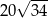Zadanie nr 9163633
Ostrosłup prawidłowy czworokątny przecięto płaszczyzna przechodzącą przez krawędź podstawy i przecinającą przeciwległe krawędzie boczne w punktach jednakowo odległych od wierzchołka ostrosłupa. Przekrój ten jest trapezem o podstawach długości 12 i 8. Oblicz pole tego przekroju, jeżeli wysokość ostrosłupa ma długość 18.
Rozwiązanie
Szkicujemy opisaną sytuację.
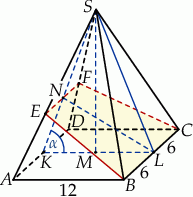
Skoro znamy długości podstaw trapezu 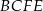 , to wystarczy obliczyć długość jego wysokości
, to wystarczy obliczyć długość jego wysokości 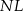 . Zrobimy to stosując twierdzenie cosinusów w trójkącie
. Zrobimy to stosując twierdzenie cosinusów w trójkącie 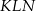 – potrzebujemy jednak do tego długość odcinka
– potrzebujemy jednak do tego długość odcinka 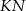 i
i 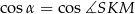 . Zacznijmy od cosinusa.
. Zacznijmy od cosinusa.
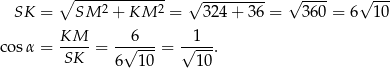
Zauważmy teraz, że trójkąty 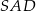 i
i 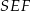 są podobne, więc
są podobne, więc

Stąd
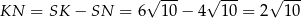
i
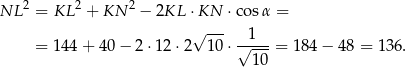
Zatem 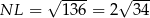 i pole trapezu
i pole trapezu 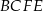 jest równe
jest równe
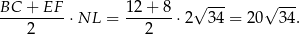
Odpowiedź: