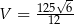Zadanie nr 9215107
W graniastosłupie prawidłowym czworokątnym 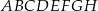 połączono punkty będące środkami krawędzi
połączono punkty będące środkami krawędzi 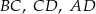 i
i 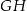 . Wyznacz objętość powstałej bryły wiedząc, że
. Wyznacz objętość powstałej bryły wiedząc, że 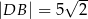 i kąt
i kąt 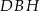 ma miarę
ma miarę 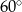 .
.
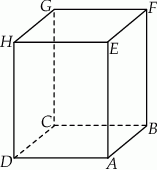
Rozwiązanie
Oznaczmy przez  długość krawędzi podstawy graniastosłupa, a przez
długość krawędzi podstawy graniastosłupa, a przez 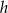 jego wysokość.
jego wysokość.
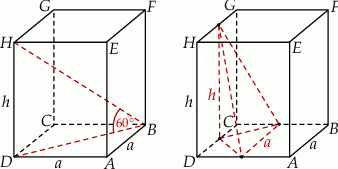
Korzystamy ze wzoru na długość przekątnej kwadratu i mamy
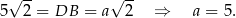
Z trójkąta prostokątnego 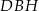 obliczamy wysokość graniastosłupa.
obliczamy wysokość graniastosłupa.
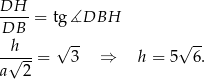
Zauważmy teraz, że ostrosłup, którego objętość mamy obliczyć ma wysokość równą 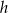 , a w podstawie ma trójkąt o podstawie
, a w podstawie ma trójkąt o podstawie  i wysokości opuszczonej na tę podstawę długości
i wysokości opuszczonej na tę podstawę długości 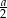 . Objętość tego ostrosłupa jest więc równa
. Objętość tego ostrosłupa jest więc równa
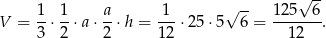
Odpowiedź: