Zadanie nr 9245204
Pole powierzchni bocznej ostrosłupa prawidłowego trójkątnego równa się 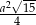 , gdzie
, gdzie  oznacza długość krawędzi podstawy tego ostrosłupa. Zaznacz na poniższym rysunku kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy. Miarę tego kąta oznacz symbolem
oznacza długość krawędzi podstawy tego ostrosłupa. Zaznacz na poniższym rysunku kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy. Miarę tego kąta oznacz symbolem 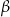 . Oblicz
. Oblicz 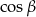 i korzystając z tablic funkcji trygonometrycznych i odczytaj przybliżoną wartość
i korzystając z tablic funkcji trygonometrycznych i odczytaj przybliżoną wartość 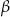 z dokładnością do
z dokładnością do 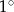 .
.
Rozwiązanie
Zaczynamy od rysunku.
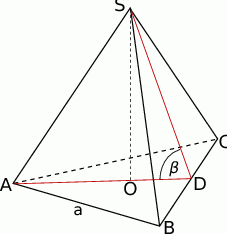
Kąt 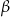 , o którym mowa w treści zadania, to kąt między wyskościami
, o którym mowa w treści zadania, to kąt między wyskościami 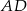 i
i 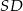 w trójkątach
w trójkątach 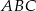 i
i 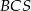 odpowiednio. Jeżeli oznaczymy
odpowiednio. Jeżeli oznaczymy 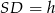 , to pole
, to pole
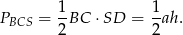
Zanim zapuścimy się w dalsze rachunki, zobaczmy co mamy wyliczyć
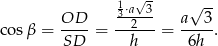
Z podanej informacji o polu powierzchni bocznej mamy
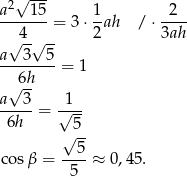
Miarę kąta 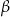 odczytujemy z tablic,
odczytujemy z tablic, 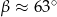 .
.
Odpowiedź: