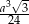Zadanie nr 9250284
W ostrosłupie prawidłowym trójkątnym długość krawędzi podstawy jest równa  i jest 4 razy większa niż odległość środka podstawy od ściany bocznej. Oblicz objętość tego ostrosłupa.
i jest 4 razy większa niż odległość środka podstawy od ściany bocznej. Oblicz objętość tego ostrosłupa.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
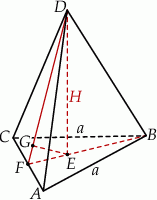
Ponieważ środek trójkąta równobocznego dzieli jego wysokość w stosunku 2:1, ze wzoru 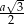 na wysokość trójkąta równobocznego mamy
na wysokość trójkąta równobocznego mamy
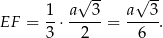
Wiemy ponadto, że 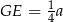 , więc możemy obliczyć długość odcinka
, więc możemy obliczyć długość odcinka 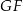 . Patrzymy na trójkąt prostokątny
. Patrzymy na trójkąt prostokątny 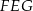 .
.
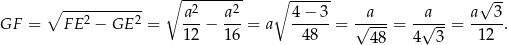
No i doszliśmy do najciekawszego momentu: zauważmy teraz, że trójkąty prostokątne 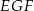 i
i 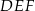 są podobne (bo mają wspólny kąt przy wierzchołku
są podobne (bo mają wspólny kąt przy wierzchołku 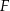 ). Z tego podobieństwa mamy
). Z tego podobieństwa mamy
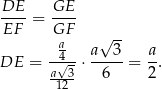
Objętość ostrosłupa jest więc równa
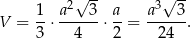
Odpowiedź: