/Szkoła średnia/Geometria/Stereometria

Zadanie nr 9339502

Dodaj do ulubionych
Dodaj do rozwiązanych

Prostokąt 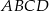ABCD obracając się wokół boku 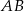AB , zakreślił walec 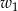w 1 . Ten sam prostokąt obracając się wokół boku 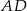AD , zakreślił walec 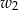w2 . Otrzymane walce mają równe pola powierzchni całkowitych. Wykaż, że prostokąt 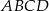ABCD jest kwadratem.

Rozwiązanie

Jeżeli naszkicujemy opisaną sytuację

PIC

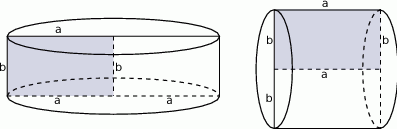
to widać, że dość łatwo możemy wyliczyć pola powierzchni całkowitej obu walców.

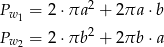
Pw1 = 2 ⋅πa 2 + 2πa ⋅b 2 Pw2 = 2 ⋅πb + 2πb ⋅a

(w każdym z wzorów pierwszy składnik to suma pól podstaw, a drugi pole powierzchni bocznej). Z równości pól powierzchni mamy równanie

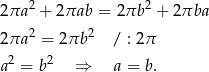
2 2 2πa + 2πab = 2πb + 2πba 2πa 2 = 2πb 2 / : 2π a2 = b2 ⇒ a = b .

Zatem boki prostokąta muszą być równe, czyli jest on kwadratem.

Wersja PDF