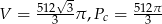/Szkoła średnia/Geometria/Stereometria

Zadanie nr 9341621

Dodaj do ulubionych
Dodaj do rozwiązanych

Wysokość podstawy graniastosłupa prawidłowego trójkątnego ma długość 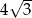√ -- 4 3 , zaś przekątna ściany bocznej tworzy z krawędzią podstawy kąt równy 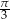π- 3 . Graniastosłup ten wpisano w walec. Oblicz pole powierzchni i objętość walca.

Rozwiązanie

Oznaczmy przez a długość podstawy, a przez wysokość graniastosłupa.

PIC

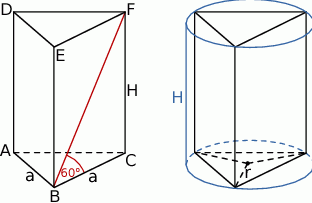
Z podanej wysokości trójkąta równobocznego w podstawie obliczamy długość krawędzi podstawy.

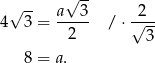
√ -- √ -- a--3- -2-- 4 3 = 2 / ⋅√ 3- 8 = a.

Teraz patrzymy na trójkąt prostokątny 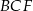BCF .

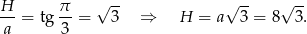
√ -- √ -- √ -- H- = tg π- = 3 ⇒ H = a 3 = 8 3. a 3

Zauważmy teraz, że walec opisany na graniastosłupie ma taką samą wysokość jak graniastosłup, a promień 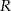R okręgu podstawy walca jest równy promieniowi okręgu opisanego na podstawie graniastosłupa, czyli

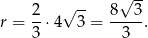
√ -- 2 √ -- 8 3 r = --⋅4 3 = ----. 3 3

Liczymy objętość i pole powierzchni walca.

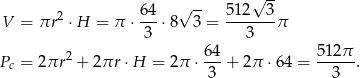
√ -- √ -- V = πr2 ⋅H = π ⋅ 6-4⋅ 8 3 = 51-2--3π 3 3 2 64- 512π-- Pc = 2πr + 2πr ⋅H = 2π ⋅ 3 + 2π ⋅64 = 3 .

 
Odpowiedź: √ - V = 512--3π,P = 512π- 3 c 3

Wersja PDF