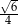Zadanie nr 9422537
Oblicz cosinus kąta między krawędzią boczną i krawędzią podstawy ostrosłupa prawidłowego trójkątnego, jeżeli wiadomo, że promień okręgu opisanego na podstawie, wysokość ostrosłupa i krawędź boczna tworzą trójkąt równoramienny.
Rozwiązanie
Rozpoczynamy od rysunku.
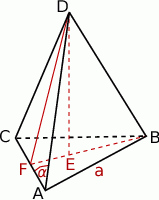
Odcinek 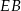 stanowi
stanowi  wysokości trójkąta równobocznego, więc jeżeli oznaczymy
wysokości trójkąta równobocznego, więc jeżeli oznaczymy 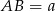 to
to
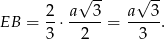
Z treści zadania wiemy, że trójkąt 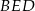 jest równoramienny. Jest on też prostokątny, więc jest to połówka kwadratu. W szczególności
jest równoramienny. Jest on też prostokątny, więc jest to połówka kwadratu. W szczególności
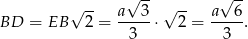
Teraz możemy obliczyć żądany cosinus.
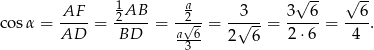
Odpowiedź: