/Szkoła średnia/Geometria/Stereometria

Zadanie nr 9512848

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole podstawy ostrosłupa prawidłowego trójkątnego jest równe 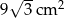√ -- 2 9 3 cm , a jego pole powierzchni bocznej jest równe 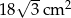√ -- 18 3 cm 2 . Oblicz objętość tego ostrosłupa.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

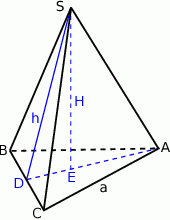
Wiemy, że trójkąt równoboczny w podstawie ma pole 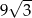√ -- 9 3 , więc mamy

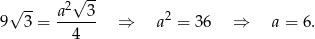
√ -- √ -- a2--3- 2 9 3 = 4 ⇒ a = 36 ⇒ a = 6.

W takim razie z podanego pola powierzchni bocznej mamy równanie

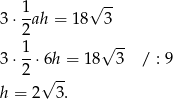
3 ⋅ 1ah = 18√ 3- 2 1 √ -- 3 ⋅--⋅6h = 18 3 / : 9 2 √ -- h = 2 3.

Obliczmy jeszcze długość odcinka 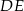DE – jest ona równa długości promienia okręgu wpisanego w postawę.

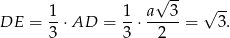
√ -- 1 1 a 3 √ -- DE = --⋅AD = --⋅-----= 3. 3 3 2

Z trójkąta prostokątnego 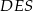DES mamy

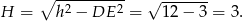
∘ ---------- ------- H = h2 − DE 2 = √ 1 2− 3 = 3.

Objętość ostrosłupa jest więc równa

1- 1- √ -- √ -- V = 3 ⋅Pp ⋅H = 3 ⋅ 9 3⋅ 3 = 9 3.

 
Odpowiedź: √ -- V = 9 3 cm 3

Wersja PDF