/Szkoła średnia/Geometria/Stereometria

Zadanie nr 9548617

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest stożek o polu powierzchni bocznej równym 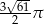3√-61 2 π , w którym tangens kąta nachylenia tworzącej do podstawy jest równy 56 . Oblicz objętość tego stożka.

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

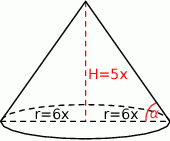
Podana informacja o tangensie kąta nachylenia tworzącej do podstawy oznacza, że

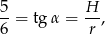
5-= tg α = H- , 6 r

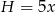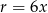więc możemy oznaczyć H = 5x i r = 6x . Obliczmy teraz długość tworzącej stożka

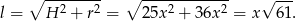
∘ -------- ∘ ------------ √ --- l = H 2 + r2 = 25x 2 + 3 6x2 = x 6 1.

Wykorzystujemy teraz podaną informację o polu powierzchni bocznej.

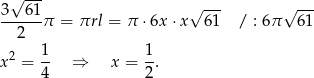
√ --- 3--61- √ --- √ --- 2 π = πrl = π ⋅6x ⋅x 6 1 / : 6π 61 1 1 x 2 = -- ⇒ x = --. 4 2

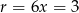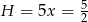Stąd r = 6x = 3 i 5 H = 5x = 2 . Liczymy teraz objętość stożka.

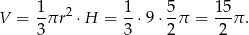
1 1 5 15 V = -πr 2 ⋅ H = --⋅9 ⋅-π = ---π . 3 3 2 2

 
Odpowiedź: 15 V = 2 π

Wersja PDF