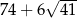Zadanie nr 9562709
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.
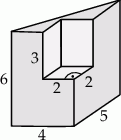
Rozwiązanie
Obliczmy najpierw objętość dużego graniastosłupa.
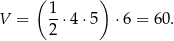
Zanim obliczymy pole powierzchni, obliczmy długość przeciwprostokątnej trójkąta w podstawie.
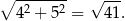
Zatem pole powierzchni jest równe
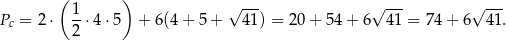
Obliczmy objętość wyciętej bryły
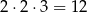
Zatem objętość bryły po wycięciu jest równa
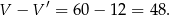
Jeżeli popatrzymy jak się zmieniło pole powierzchni, to łatwo zauważyć, że się nie zmieniło – dodaliśmy tyle samo co wycięliśmy.
Odpowiedź: Objętość: 48, pole powierzchni: