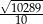Zadanie nr 9584258
Podstawą ostrosłupa trójkątnego 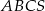 jest trójkąt prostokątny
jest trójkąt prostokątny 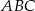 , w którym
, w którym 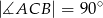 i
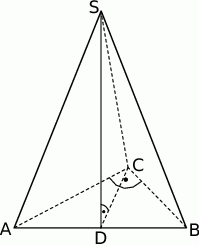
i 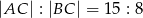 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 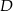 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 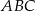 , a odcinek
, a odcinek 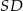 jest wysokością ostrosłupa. Objętość ostrosłupa jest równa 8, a pole ściany
jest wysokością ostrosłupa. Objętość ostrosłupa jest równa 8, a pole ściany 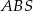 jest równe 17. Oblicz długość krawędzi
jest równe 17. Oblicz długość krawędzi 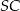 ostrosłupa
ostrosłupa
Rozwiązanie
Podany stosunek długości przyprostokątnych trójkąta 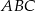 pozwala nam oznaczyć
pozwala nam oznaczyć 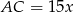 i
i 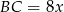 . Na mocy twierdzenia Pitagorasa mamy
. Na mocy twierdzenia Pitagorasa mamy
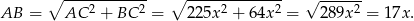
Oznaczmy teraz 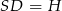 i zapiszmy podane informacje o objętości ostrosłupa i polu powierzchni ściany
i zapiszmy podane informacje o objętości ostrosłupa i polu powierzchni ściany 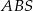 .
.
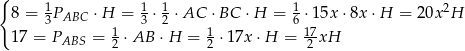
Z drugiego równania mamy 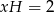 i pierwsze równanie przyjmuje postać
i pierwsze równanie przyjmuje postać
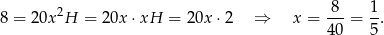
Stąd
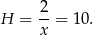
Zauważmy teraz, że środek okręgu opisanego na trójkącie prostokątnym to dokładnie środek przeciwprostokątnej (przeciwprostokątna jest średnicą tego okręgu). Zatem
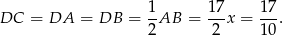
Pozostało teraz zastosować twierdzenie Pitagorasa w trójkącie prostokątnym 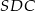 .
.
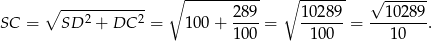
Odpowiedź: