/Szkoła średnia/Geometria/Stereometria

Zadanie nr 9588552

Dodaj do ulubionych
Dodaj do rozwiązanych

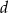W ostrosłupie prawidłowym trójkątnym kąt płaski przy wierzchołku ostrosłupa ma miarę α , zaś odległość wierzchołka podstawy od krawędzi bocznej, do której nie należy, jest równa d . Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

Rozwiązanie

Zaczynamy od rysunku.

PIC

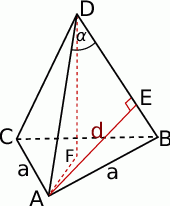
Najpierw, z trójkąta 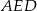AED , wyliczymy długość krawędzi bocznej ostrosłupa.

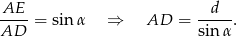
AE--= sinα ⇒ AD = --d--. AD sinα

Ponieważ trójkąt 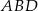ABD jest równoramienny, mamy 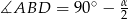∡ABD = 90∘ − α2 . Zatem z trójkąta 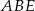ABE mamy

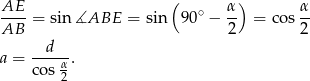
( ) AE--= sin ∡ABE = sin 9 0∘ − α- = cos α- AB 2 2 d a = ----α. cos 2

Teraz z trójkąta 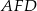AF D wyliczymy długość wysokości ostrosłupa. Aby to zrobić zauważmy, że odcinek 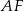AF to 23 wysokości trójkąta równobocznego w podstawie, czyli

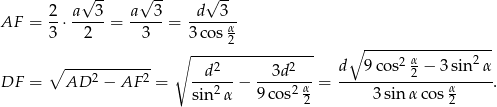
√ -- √ -- √ -- 2- a--3- a--3- -d--3-- AF = 3 ⋅ 2 = 3 = 3cos α 2 ∘ ------------------ ∘ ------------ ∘ ---2----------2-- d 9co s2 α − 3 sin 2α DF = AD 2 − AF 2 = --d---− --3d----= ----------2----------. sin2 α 9 cos2 α2 3sin αco s α2

Możemy teraz policzyć objętość (korzystamy ze wzoru na pole trójkąta równobocznego).

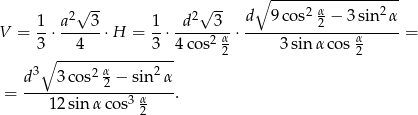
∘ ------------------ 2√ -- 2√ -- d 9 cos2 α− 3sin2 α V = 1-⋅ a---3-⋅H = 1-⋅-d----3- ⋅----------2---------- = 3 4 3 4 cos2 α2 3sinα cos α2 ∘ ---------------- d3 3 cos2 α2 − sin2 α = --------------3-α---. 12 sin α cos 2

Teraz policzymy pole powierzchni bocznej.

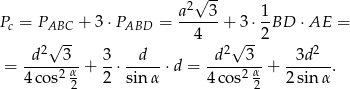
2√ -- P = P + 3 ⋅P = a---3+ 3⋅ 1BD ⋅AE = c ABC ABD 4 2 d 2√ 3- 3 d d 2√ 3- 3d2 = -----2-α + --⋅----- ⋅d = -----2-α + ------. 4 cos 2 2 sin α 4 cos 2 2 sin α

 
Odpowiedź: √ ------------ √ - V = d3--3cos2-α2−sin2α-, P = -d2--3-+ -3d2- 12 sinαcos3 α2 c 4cos2 α2 2sinα

Wersja PDF