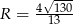/Szkoła średnia/Geometria/Stereometria

Zadanie nr 9606162

Dodaj do ulubionych
Dodaj do rozwiązanych

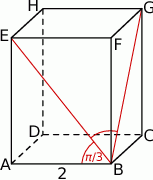
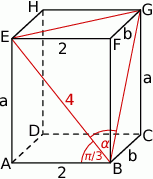
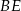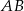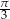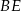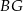Przekątna BE ściany bocznej prostopadłościanu ABCDEF GH tworzy z krawędzią podstawy AB kąt o mierze π3- . Przekątne BE i BG ścian bocznych tworzą kąt, którego cosinus jest równy 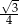√ - --3 4 , a krawędź 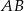AB podstawy ma długość 2. Oblicz promień okręgu opisanego na trójkącie EBG .

PIC

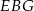Rozwiązanie

Oznaczmy 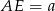AE = a i BC = b .

PIC

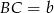W trójkącie prostokątnym 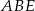ABE mamy

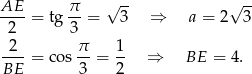
√ -- √ -- AE--= tg π- = 3 ⇒ a = 2 3 2 3 -2- π- 1- BE = cos 3 = 2 ⇒ BE = 4 .

Napiszmy teraz twierdzenie cosinusów w trójkącie 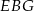EBG .

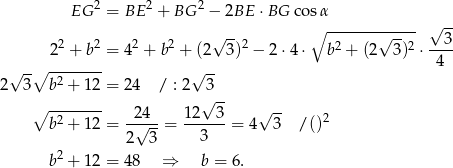
EG 2 = BE 2 + BG 2 − 2BE ⋅BG cos α √ -- ∘ -------√----- √ -- 22 + b2 = 42 + b2 + (2 3)2 − 2⋅ 4⋅ b2 + (2 3)2 ⋅--3- -∘ -------- -- 4 2√ 3 b2 + 12 = 24 / : 2√ 3 √ -- ∘ -2------ -24-- 12--3- √ -- 2 b + 12 = √ --= 3 = 4 3 /() 2 3 b2 + 12 = 48 ⇒ b = 6.

Stąd

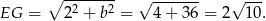
∘ -2----2 √ ------- √ --- EG = 2 + b = 4+ 36 = 2 10 .

Obliczamy jeszcze 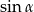sin α (żeby móc skorzystać z twierdzenia sinusów).

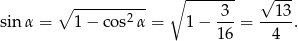
∘ ---------- ∘ ------- √ --- sin α = 1− cos2α = 1 − -3-= --13-. 16 4

Pozostało teraz skorzystać z twierdzenia sinusów w trójkącie EBG .

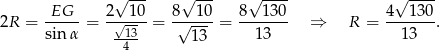
√ --- √ --- √ ---- √ ---- 2R = -EG-- = 2√--10 = 8√--10 = 8--130- ⇒ R = 4--130. sinα --13 13 13 13 4

 
Odpowiedź: √ --- R = 4--130 13

Wersja PDF