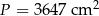/Szkoła średnia/Geometria/Stereometria

Zadanie nr 9615259

Dodaj do ulubionych
Dodaj do rozwiązanych

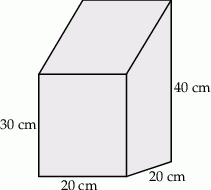
Spawacz ma wykonać z blachy konstrukcję, której podstawą jest kwadrat a ściany boczne są prostopadłe do płaszczyzny podstawy. Wymiary elementów są podane na rysunku. Oblicz pole powierzchni tej konstrukcji (wszystkich sześciu ścian). Wynik podaj z zaokrągleniem do 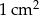1 cm 2 .

PIC

Rozwiązanie

Powierzchnia konstrukcji składa się z:

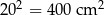  • kwadratu w podstawie, pole: 202 = 4 00 cm 2 ,
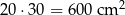  • prostokąta z przodu, pole: 20 ⋅30 = 60 0 cm 2 ,
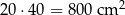  • prostokąta z tyłu, pole: 20⋅4 0 = 800 cm 2 ,
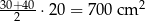  • dwóch trapezów o polu: 30+40 2 2 ⋅20 = 70 0 cm ,
  • prostokąta u góry, jego skośny bok ma długość
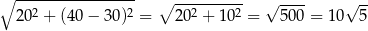
    ∘ ----------------- ∘ ---------- √ ---- √ -- 202 + (40− 30)2 = 2 02 + 1 02 = 500 = 1 0 5

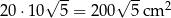    (twierdzenie Pitagorasa), a pole: √ -- √ -- 20⋅1 0 5 = 200 5 cm 2 .

Zatem pole powierzchni całkowitej:

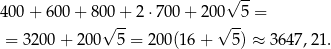
√ -- 400 + 6 00+ 800 + 2⋅ 700+ 200 5 = √ -- √ -- = 3 200+ 200 5 = 200(16 + 5) ≈ 3 647,21.

Po zaokrągleniu 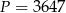P = 3647 .  
Odpowiedź: P = 3647 cm 2

Wersja PDF