/Szkoła średnia/Geometria/Stereometria

Zadanie nr 9620169

Dodaj do ulubionych
Dodaj do rozwiązanych

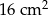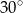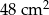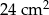Dany jest graniastosłup, którego podstawą jest równoległobok o polu 2 16 cm i kącie ostrym 30∘ . Oblicz objętość graniastosłupa jeżeli pola jego ścian są równe 48 cm 2 i 24 cm 2 .

Rozwiązanie

Zaczynamy od schematycznego rysunku i oznaczmy krawędzie podstawy przez 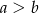a > b , a wysokość przez H .

PIC

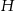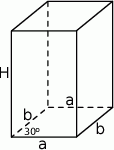
Ze wzoru z sinusem na pole równoległoboku mamy

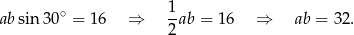
absin 30∘ = 16 ⇒ 1ab = 16 ⇒ ab = 3 2. 2

Z pól ścian bocznych mamy

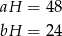
aH = 48 bH = 24

Mnożąc te równości stronami i korzystając z równości 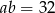ab = 32 mamy

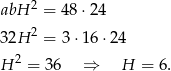
abH 2 = 48⋅2 4 2 32H = 3⋅1 6⋅24 H 2 = 3 6 ⇒ H = 6.

Zatem objętość graniastosłupa wynosi

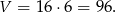
V = 16 ⋅6 = 96.

 
Odpowiedź: 3 96 cm

Wersja PDF