/Szkoła średnia/Geometria/Stereometria

Zadanie nr 9691202

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość 6, a pole ściany bocznej jest równe 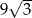√ -- 9 3 . Oblicz objętość tego ostrosłupa.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

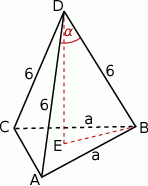
Aby wykorzystać podaną informację o polu powierzchni ściany bocznej piszemy dla ściany 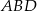ABD wzór na pole z sinusem.

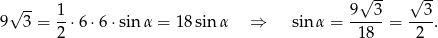
√ -- √ -- √ -- 1- 9--3- --3- 9 3 = 2 ⋅6⋅ 6⋅sin α = 18 sin α ⇒ sinα = 18 = 2 .

Zatem 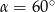∘ α = 6 0 , co oznacza, że ściany boczne to trójkąty równoboczne.

Wysokość ostrosłupa wyliczymy z trójkąta prostokątnego 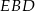EBD – zanim jednak to zrobimy, wyliczmy długość odcinka 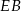EB . Stanowi on 23 wysokości podstawy, wiec ze wzoru na wysokość w trójkącie równobocznym mamy

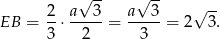
√ -- √ -- 2 a 3 a 3 √ -- EB = --⋅ -----= ----- = 2 3. 3 2 3

Stąd

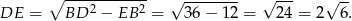
∘ ---2------2- √ -------- √ --- √ -- DE = BD − EB = 36 − 12 = 24 = 2 6.

Objętość ostrosłupa jet więc równa

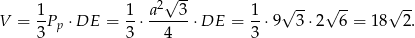
1 1 a2√ 3- 1 √ -- √ -- √ -- V = -Pp ⋅DE = --⋅------⋅DE = --⋅9 3 ⋅2 6 = 18 2. 3 3 4 3

 
Odpowiedź: √ -- 18 2

Wersja PDF