Zadanie nr 9745121
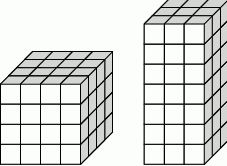
Jacek bawi się sześciennymi klockami o krawędzi 2 cm. Zbudował z nich jeden duży sześcian o krawędzi 8 cm i wykorzystał do tego wszystkie swoje klocki. Następnie zburzył budowlę i ułożył z tych klocków drugą bryłę – graniastosłup prawidłowy czworokątny. Wtedy okazało się, że został mu dokładnie jeden klocek, którego nie było gdzie dołożyć. Oblicz stosunek pola powierzchni całkowitej pierwszej ułożonej bryły do pola powierzchni całkowitej drugiej bryły i wynik podaj w postaci ułamka nieskracalnego.
Rozwiązanie
Objętość małego sześcianu to
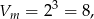
a objętość dużego to
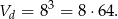
W takim razie Jacek ma 64 klocki. To z kolei oznacza, że graniastosłup prawidłowy czworokątny zbudował z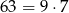 
klocków. Graniastosłup ten nie mógł mieć w podstawie jednego klocka, bo wtedy można by do niego dołożyć 64 klocek. W takim razie w podstawie musiał mieć 9 klocków i był wysoki na 7 klocków (liczba klocków w podstawie musi być kwadratem liczby naturalnej).
Na powierzchni graniastosłupa jest więc
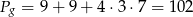
kwadratów o boku 2 cm. Na powierzchni sześcianu jest z kolei
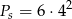
takich kwadratów. W takim razie interesujący nas stosunek powierzchni brył jest równy
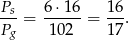
Odpowiedź: 
