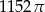Zadanie nr 9877022
W pojemniku o kształcie walca o promieniu podstawy 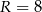 umieszczono dwie kule o promieniu
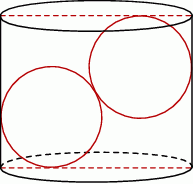
umieszczono dwie kule o promieniu 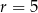 , w ten sposób, że są do siebie styczne i każda z nich dotyka powierzchni bocznej walca, jak na rysunku. Jaka co najmniej musi być wysokość pojemnika, aby kule całkowicie się w nim mieściły. Oblicz objętość tego walca.
, w ten sposób, że są do siebie styczne i każda z nich dotyka powierzchni bocznej walca, jak na rysunku. Jaka co najmniej musi być wysokość pojemnika, aby kule całkowicie się w nim mieściły. Oblicz objętość tego walca.
Rozwiązanie
Zaczynamy od rysunku.
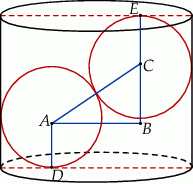
W pojemniku o najmniejszej wysokości kule są do siebie styczne oraz są styczne do podstaw pojemnika. Wysokość pojemnika możemy podzielić na trzy odcinki 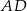 ,
, 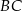 i
i 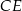 . Pierwszy i trzeci mają długość
. Pierwszy i trzeci mają długość 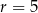 a długość drugiego możemy obliczyć z trójkąta prostokątnego
a długość drugiego możemy obliczyć z trójkąta prostokątnego 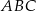 . Zauważmy, że długość odcinka
. Zauważmy, że długość odcinka 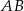 to średnica podstawy walca minus dwa promienie wpisanych kul. Zatem
to średnica podstawy walca minus dwa promienie wpisanych kul. Zatem
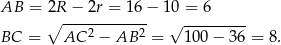
Zatem wysokość walca wynosi
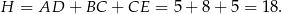
Liczymy objętość
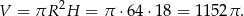
Odpowiedź: Wysokość: 18, objętość: