/Szkoła średnia/Geometria/Stereometria

Zadanie nr 9979646

Dodaj do ulubionych
Dodaj do rozwiązanych

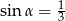Krawędź boczna ostrosłupa prawidłowego czworokątnego jest nachylona do płaszczyzny podstawy pod kątem α takim, że sin α = 13 . Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.

Rozwiązanie

Zaczynamy od rysunku

PIC

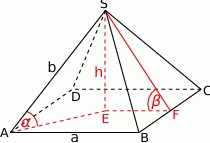
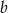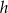Oznaczmy długość krawędzi bocznej przez b , długość krawędzi podstawy przez a i długość wysokości ostrosłupa przez h . Z podanego sinusa kąta nachylenia krawędzi bocznej mamy

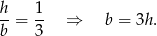
h- 1- b = 3 ⇒ b = 3h.

Zatem

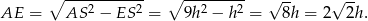
∘ ----------- ∘ --------- √ -- √ -- AE = AS 2 − ES2 = 9h2 − h2 = 8h = 2 2h.

Odcinek 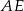AE to połowa przekątnej kwadratu, więc

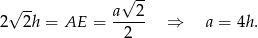
√ -- √ -- a--2- 2 2h = AE = 2 ⇒ a = 4h.

Teraz możemy wyliczyć długość wysokości ściany bocznej – patrzymy na trójkąt prostokątny 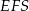EF S .

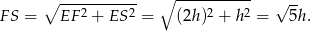
∘ ----------- ∘ ---2-----2- 2 2 √ -- FS = EF + ES = (2h) + h = 5h .

Zatem

√ -- cosβ = EF- = √2h-- = √2---= 2--5-. FS 5h 5 5

 
Odpowiedź: √ - 2--5 5

Wersja PDF