/Szkoła średnia/Geometria/Stereometria

Zadanie nr 9983894

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłupie prawidłowym trójkątnym wysokość ściany bocznej ma długość 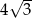√ -- 4 3 , a ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 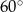60 ∘ . Oblicz objętość ostrosłupa.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

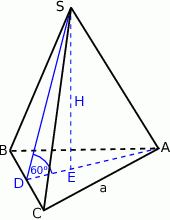
Zauważmy, że podany kąt nachylenia ściany bocznej do podstawy pozwala łatwo obliczyć długość wysokości 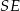SE ostrosłupa oraz promień 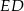ED okręgu wpisanego w trójkąt równoboczny w podstawie. Patrzymy na trójkąt prostokątny SDE .

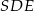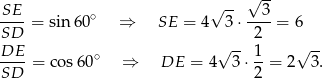
-- SE √ -- √ 3 ----= sin 60∘ ⇒ SE = 4 3⋅ ----= 6 SD 2 DE--= cos6 0∘ ⇒ DE = 4√ 3⋅ 1-= 2√ 3-. SD 2

Promień okręgu wpisanego w trójkąt równoboczny to 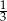13 jego wysokości, więc jeżeli oznaczymy przez a długość krawędzi postawy to mamy równanie

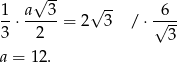
√ -- 1 a 3 √ -- 6 --⋅-----= 2 3 / ⋅ √--- 3 2 3 a = 12.

Pozostało obliczyć objętość ostrosłupa

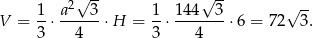
√ -- √ -- 1 a2 3 1 144 3 √ -- V = --⋅------⋅H = --⋅ -------⋅6 = 7 2 3. 3 4 3 4

 
Odpowiedź: √ -- V = 72 3

Wersja PDF