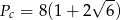Zadanie nr 9999616
Objętość graniastosłupa prawidłowego czworokątnego jest równa 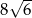 . Przekątna tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
. Przekątna tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 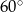 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.
Rozwiązanie
Rozpoczynamy od rysunku.
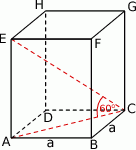
Oznaczmy przez  długość krawędzi podstawy graniastosłupa. Korzystając ze wzoru na długość przekątnej kwadratu mamy
długość krawędzi podstawy graniastosłupa. Korzystając ze wzoru na długość przekątnej kwadratu mamy
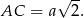
Z trójkąta prostokątnego 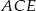 obliczamy wysokość graniastosłupa.
obliczamy wysokość graniastosłupa.
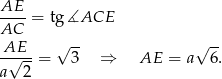
Teraz wykorzystujemy informację o objętości graniastosłupa.
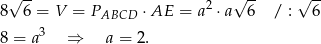
Pozostało obliczyć pole powierzchni całkowitej graniastosłupa.
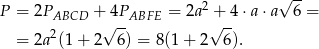
Odpowiedź: