Zadanie nr 2189527
Oblicz pole rombu, którego jeden z kątów wewnętrznych wynosi 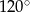 , a przekątna poprowadzona z wierzchołka tego kąta ma długość 10 cm.
, a przekątna poprowadzona z wierzchołka tego kąta ma długość 10 cm.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
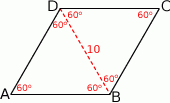
Ponieważ przekątne rombu są dwusiecznymi kątów wewnętrznych, mamy
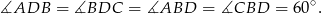
To oznacza, że trójkąty 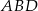 i
i 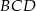 są trójkątami równobocznymi o boku długości
są trójkątami równobocznymi o boku długości 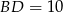 . Pole rombu jest więc równe
. Pole rombu jest więc równe
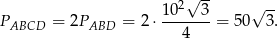
Odpowiedź: