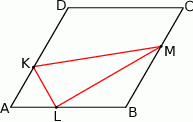
Zadanie nr 5766276
Na bokach 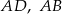 i
i 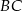 rombu
rombu 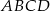 wybrano punkty
wybrano punkty 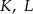 i
i 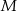 w ten sposób, że
w ten sposób, że 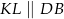 i
i 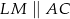 . Uzasadnij, że pole czworokąta
. Uzasadnij, że pole czworokąta 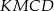 stanowi połowę pola rombu.
stanowi połowę pola rombu.
Rozwiązanie
Oznaczmy przez  długość boku rombu oraz niech
długość boku rombu oraz niech 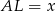 .
.
Po pierwsze zauważmy, że z równoległości 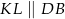 wynika, że trójkąty
wynika, że trójkąty 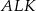 i
i 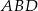 są podobne. W szczególności trójkąt
są podobne. W szczególności trójkąt 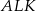 jest równoramienny
jest równoramienny 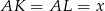 . Analogicznie uzasadniamy (patrząc na trójkąty
. Analogicznie uzasadniamy (patrząc na trójkąty 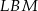 i
i 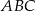 ), że trójkąt
), że trójkąt 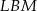 jest równoramienny,
jest równoramienny, 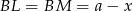 . W takim razie
. W takim razie
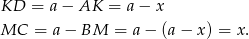
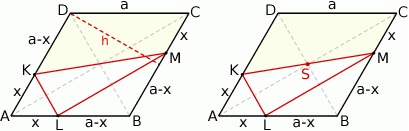
Sposób I
Czworokąt 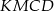 jest trapezem o podstawach
jest trapezem o podstawach 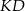 i
i 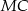 oraz wysokość
oraz wysokość 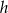 równej wysokości rombu. Jego pole jest więc równe
równej wysokości rombu. Jego pole jest więc równe
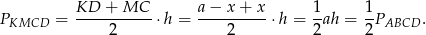
Sposób II
Z warunku 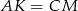 wynika, że prosta
wynika, że prosta 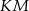 przechodzi przez środek symetrii
przechodzi przez środek symetrii 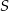 rombu (czyli przez punkt przecięcia się przekątnych). W szczególności w symetrii środkowej względem punktu
rombu (czyli przez punkt przecięcia się przekątnych). W szczególności w symetrii środkowej względem punktu 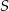 punkty
punkty 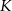 i
i 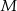 zamieniają się miejscami, czyli czworokąt
zamieniają się miejscami, czyli czworokąt 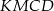 przechodzi na czworokąt
przechodzi na czworokąt 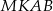 . To oznacza, że te dwa czworokąty mają równe pola, więc pole każdego z nich musi stanowić połowę pola rombu.
. To oznacza, że te dwa czworokąty mają równe pola, więc pole każdego z nich musi stanowić połowę pola rombu.

