/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2025/Próbne testy
Próbny Egzamin Ósmoklasisty
z Matematyki CKE 3 grudnia 2024 Czas pracy: 100 minut
Poniżej zamieszczono fragment etykiety pewnego opakowania śmietany.
| Wartość odżywcza | w 100 g |
| tłuszcz | 18 g |
| węglowodany | 4 g |
| białko | 3 g |
| sól | 0,15 g |
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
W opakowaniu zawierającym 200 g tej śmietany jest A/B dag białka.
A) 0,6 B) 0,06
Masa tłuszczu w dowolnej porcji tej śmietany jest C/D razy większa od masy soli.
C) 12 D) 120
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wartość wyrażenia 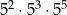 jest równa jest równa 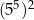 . . | P | F |
Wyrażenia 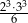 oraz oraz 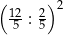 mają taką samą wartość. mają taką samą wartość. | P | F |
Wyrażenie 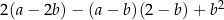 można przekształcić równoważnie do postaci
można przekształcić równoważnie do postaci
A) 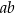 B)
B)  C)
C) 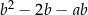 D)
D) 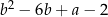 E)
E) 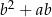
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Liczba 4 jest mniejsza od liczby A/B .
A) 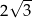 B)
B) 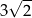
Liczba 4 jest większa od liczby C/D .
C) 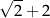 D)
D) 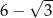
W pudełku znajdują się kule różniące się tylko kolorem: białe, czerwone i niebieskie. Kul białych jest pięć, kul czerwonych jest trzy razy więcej niż białych, a kul niebieskich jest o pięć mniej niż czerwonych. Z pudełka losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli białej jest równe
A)  B)
B)  C)
C)  D)
D) 
Dana jest nierówność 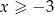 . Na którym rysunku poprawnie zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych
. Na którym rysunku poprawnie zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych  spełniających tę nierówność?
spełniających tę nierówność?
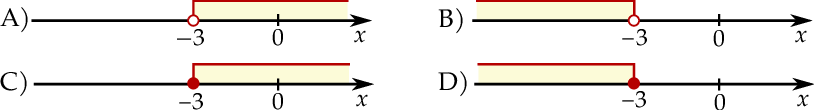
Uczniom klas ósmych zadano pytanie: Z którego portalu internetowego korzystasz najczęściej?. Każdy z uczniów wskazał jeden portal. Procentowy rozkład udzielonych odpowiedzi uczniów przedstawiono na diagramie poniżej. Portal  wskazało 72 uczniów.
wskazało 72 uczniów.
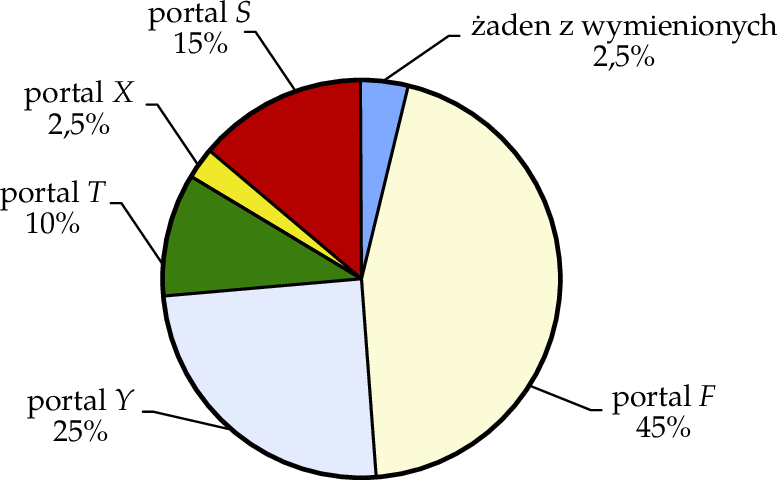
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Portal 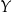 wskazało 40 uczniów. wskazało 40 uczniów. | P | F |
Portal 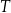 wskazało o 8 uczniów mniej niż uczniów, którzy wskazali portal wskazało o 8 uczniów mniej niż uczniów, którzy wskazali portal 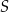 . . | P | F |
Dane są cztery liczby: 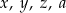 . Wiadomo, że
. Wiadomo, że 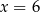 ,
, 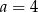 oraz średnia arytmetyczna trzech liczb
oraz średnia arytmetyczna trzech liczb 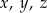 jest równa 12. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
jest równa 12. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Średnia arytmetyczna dwóch liczb 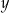 i
i  jest równa A/B .
jest równa A/B .
A) 6 B) 15
Średnia arytmetyczna czterech liczb: 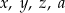 , jest równa C/D .
, jest równa C/D .
C) 8 D) 10
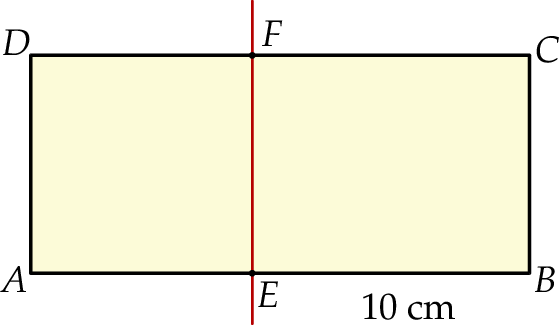
Prostokąt 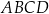 podzielono prostą
podzielono prostą 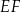 na kwadrat
na kwadrat 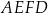 i prostokąt
i prostokąt 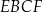 (zobacz rysunek). Obwód prostokąta
(zobacz rysunek). Obwód prostokąta 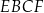 jest równy 36 cm, a długość boku
jest równy 36 cm, a długość boku 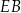 jest równa 10 cm.
jest równa 10 cm.
Pole kwadratu 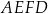 jest równe
jest równe
A)  B)
B) 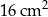 C)
C) 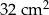 D)
D) 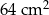
Na rysunku przedstawiono proste 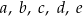 oraz zaznaczono miary niektórych kątów. Proste
oraz zaznaczono miary niektórych kątów. Proste 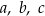 są wzajemnie równoległe. Proste
są wzajemnie równoległe. Proste 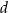 i
i  są wzajemnie prostopadłe i przecinają się w punkcie
są wzajemnie prostopadłe i przecinają się w punkcie 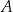 leżącym na prostej
leżącym na prostej 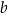 .
.
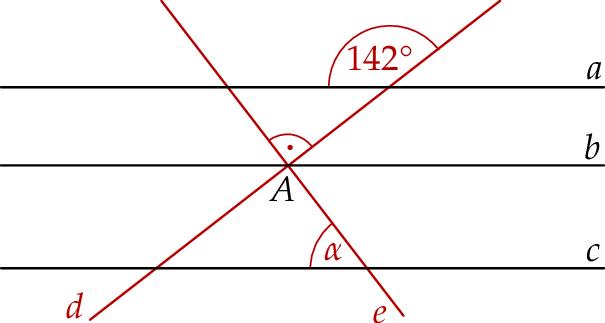
Miara kąta  jest równa
jest równa
A) 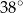 B)
B) 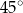 C)
C) 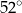 D)
D) 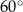
Dany jest romb, którego przekątne mają długość 24 cm i 18 cm. Pole tego rombu jest równe
A) 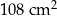 B)
B) 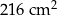 C)
C) 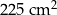 D)
D) 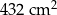
Na rysunku przedstawiono dwa trójkąty: 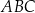 i
i 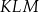 , podano długości boków
, podano długości boków 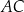 i
i 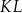 oraz zaznaczono miary niektórych kątów.
oraz zaznaczono miary niektórych kątów.
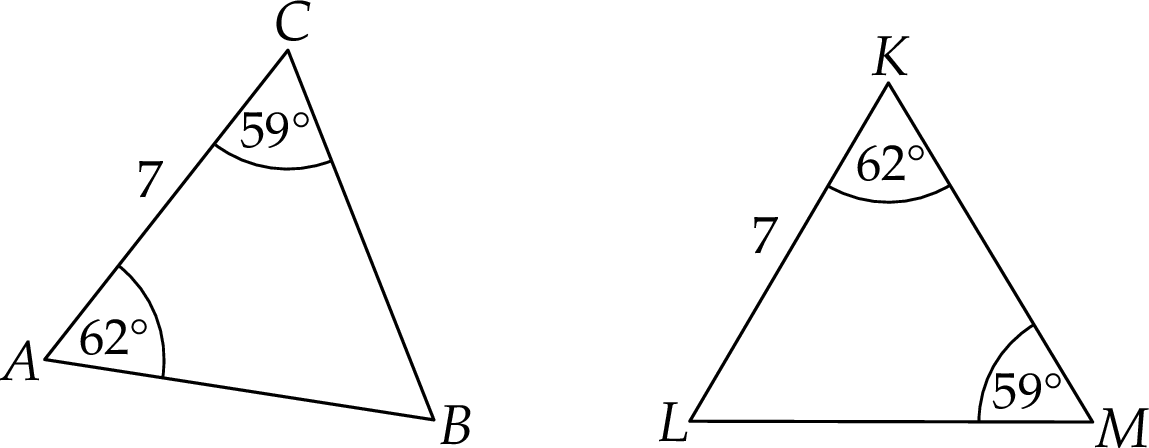
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 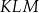 nie jest równoramienny. nie jest równoramienny. | P | F |
Trójkąty 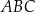 i i  są przystające. są przystające. | P | F |
Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 7. Krawędź boczna tego graniastosłupa jest dwa razy dłuższa od krawędzi podstawy. Objętość tego graniastosłupa jest równa
A) 686 B) 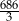 C) 343 D)
C) 343 D) 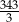
Odcinkowy pomiar prędkości polega na wyznaczeniu średniej prędkości samochodu na określonym odcinku drogi. Na początku i na końcu takiego odcinka ustawiono znaki drogowe informujące o rozpoczęciu i zakończeniu pomiaru (zobacz rysunek).

Samochód osobowy przejechał w 2 minuty taki odcinek drogi o długości 3 km. Wyznaczona prędkość tego samochodu na objętym pomiarem odcinku drogi była równa
A) 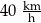 B)
B) 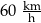 C)
C) 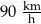 D)
D) 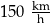
Dany jest okrąg  , którego średnica ma długość 20 cm. Odcinek
, którego średnica ma długość 20 cm. Odcinek 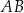 ma długość 12 cm i jest cięciwą tego okręgu. Punkty
ma długość 12 cm i jest cięciwą tego okręgu. Punkty 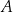 i
i 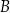 połączono z punktem
połączono z punktem 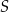 , który jest środkiem tego okręgu (zobacz rysunek).
, który jest środkiem tego okręgu (zobacz rysunek).

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Obwód trójkąta 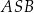 jest równy 36 cm. jest równy 36 cm. | P | F |
Długość okręgu  jest równa jest równa 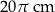 . . | P | F |
Na festyn wpuszczano uczestników jednym wejściem. Pierwszy wchodzący otrzymał i sok, i ciastko. Następnie co szósty wchodzący otrzymywał sok, a co dziesiąty wchodzący otrzymywał ciastko. To znaczy, że sok otrzymali wchodzący: pierwszy, siódmy, trzynasty itd. A ciastko otrzymali wchodzący: pierwszy, jedenasty, dwudziesty pierwszy itd. Na festyn przyszło 450 osób. Oblicz, ilu uczestników tego festynu otrzymało i sok, i ciastko.
Dany jest trójkąt 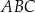 , w którym długości boków opisano za pomocą wyrażeń algebraicznych (zobacz rysunek).
, w którym długości boków opisano za pomocą wyrażeń algebraicznych (zobacz rysunek).
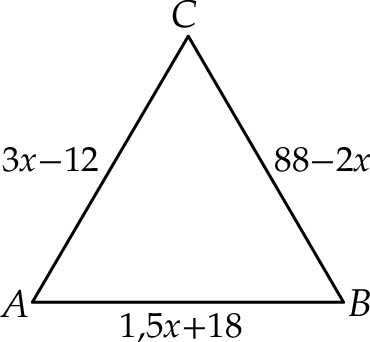
Długość boku 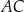 w tym trójkącie jest równa długości boku
w tym trójkącie jest równa długości boku 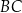 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 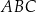 jest równoboczny.
jest równoboczny.
Na rysunku przedstawiono trapez równoramienny 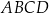 , w którym
, w którym 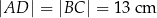 .
.
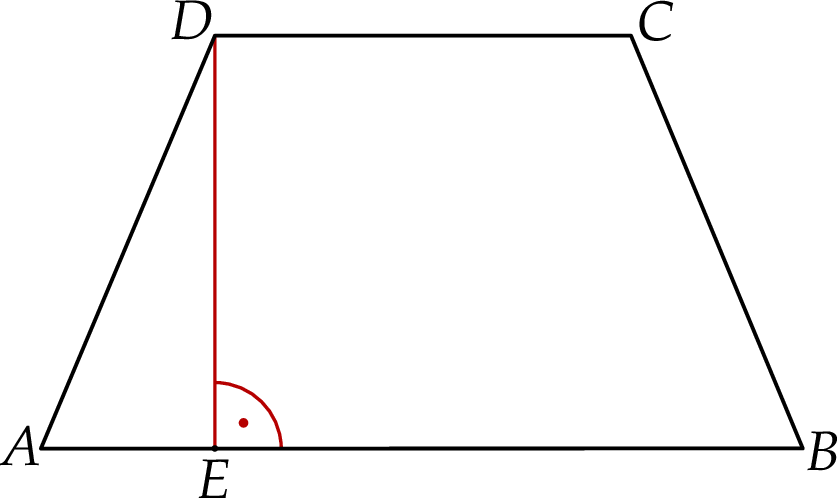
Wysokość 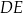 oraz krótsza podstawa
oraz krótsza podstawa 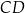 mają długość po 12 cm. Oblicz pole trapezu
mają długość po 12 cm. Oblicz pole trapezu 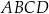 .
.
Marek kupił w sklepie sportowym kask narciarski, buty i narty. Kask kosztował 500 zł. Narty i kask kosztowały razem o 700 zł mniej niż narty i buty łącznie. Buty i kask kosztowały razem tyle co narty. Oblicz, ile kosztowały narty, a ile kosztowały buty, które kupił Marek w tym sklepie.
Na rysunku przedstawiono siatkę graniastosłupa prawidłowego czworokątnego oraz zapisano jeden z wymiarów tej siatki. Wysokość  tego graniastosłupa jest 1,5 razy większa od długości krawędzi podstawy.
tego graniastosłupa jest 1,5 razy większa od długości krawędzi podstawy.
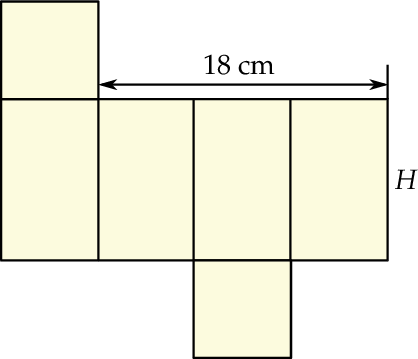
Oblicz pole powierzchni bocznej tego graniastosłupa.
Urządzenie do produkcji kostek lodu nalewa wodę do jednakowych foremek w kształcie sześcianu o pojemności 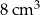 . Wlana woda wypełnia 75% pojemności każdej foremki. Z jednej foremki zostanie wyprodukowana jedna kostka lodu. Oblicz, ile kostek lodu wyprodukuje to urządzenie z
. Wlana woda wypełnia 75% pojemności każdej foremki. Z jednej foremki zostanie wyprodukowana jedna kostka lodu. Oblicz, ile kostek lodu wyprodukuje to urządzenie z 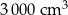 wody.
wody.

