/Szkoła średnia/Zadania maturalne/Matura 2025/Matura próbna
Próbny Egzamin Maturalny
z Matematyki (CKE)
poziom podstawowy 6 grudnia 2024 Czas pracy: 180 minut
Liczby 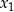 i
i 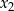 są różnymi rozwiązaniami równania
są różnymi rozwiązaniami równania 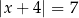 . Suma
. Suma 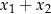 jest równa
jest równa
A) 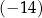 B)
B) 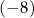 C) 3 D) 8
C) 3 D) 8
Liczba 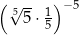 jest równa
jest równa
A) 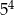 B)
B) 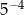 C)
C) 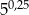 D)
D) 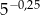
Wykaż, że liczba 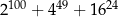 jest podzielna przez 21.
jest podzielna przez 21.
Dla każdej dodatniej liczby rzeczywistej  i dla każdej dodatniej liczby rzeczywistej
i dla każdej dodatniej liczby rzeczywistej 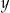 wartość wyrażenia
wartość wyrażenia 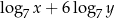 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A) 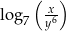 B)
B) 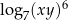 C)
C) 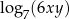 D)
D) 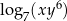
Pani Aniela wpłaciła do banku kwotę 60 000 zł na lokatę dwuletnią. Po każdym rocznym okresie oszczędzania bank doliczał odsetki w wysokości 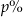 w skali roku od kwoty bieżącego kapitału znajdującego się na lokacie – zgodnie z procentem składanym. Na koniec okresu oszczędzania kwota na tej lokacie była równa 67 925,76 zł wraz z odsetkami (bez uwzględniania podatków). Oprocentowanie lokaty w skali roku było równe
w skali roku od kwoty bieżącego kapitału znajdującego się na lokacie – zgodnie z procentem składanym. Na koniec okresu oszczędzania kwota na tej lokacie była równa 67 925,76 zł wraz z odsetkami (bez uwzględniania podatków). Oprocentowanie lokaty w skali roku było równe
A) 6% B) 6,4% C) 6,5% D) 7%
Dla każdej liczby rzeczywistej  różnej od
różnej od 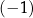 , 0 oraz 1 wartość wyrażenia
, 0 oraz 1 wartość wyrażenia 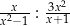 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A) 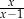 B)
B) 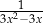 C)
C) 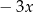 D)
D) 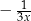
Para liczb 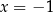 i
i 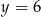 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
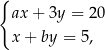
gdzie  oraz
oraz 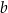 są liczbami rzeczywistymi. Wartość wyrażenia
są liczbami rzeczywistymi. Wartość wyrażenia 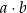 jest równa
jest równa
A) 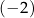 B)
B) 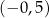 C) 0,5 D) 2
C) 0,5 D) 2
Rozwiąż równanie 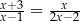 .
.
Rozwiąż nierówność 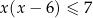 .
.
Funkcja 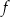 jest określona następująco
jest określona następująco
![(| { 3 dla x ∈ (− 4,− 2] f(x) = −x + 1 dla x ∈ (− 2,2] |( x− 3 dla x ∈ (2,4]](https://img.zadania.info/zes/0091818/HzesT38x.png)
Wykres funkcji 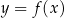 przedstawiono w kartezjańskim układzie współrzędnych
przedstawiono w kartezjańskim układzie współrzędnych 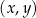 na rysunku poniżej.
na rysunku poniżej.
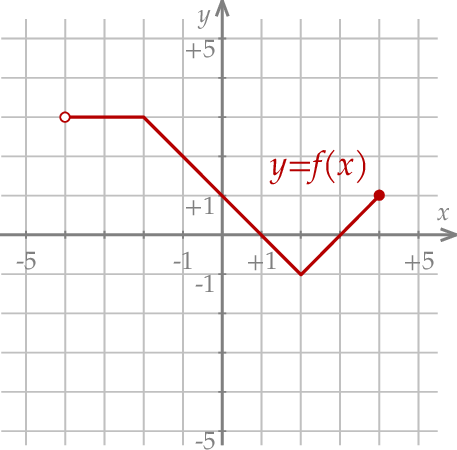
-
Wyznacz dziedzinę funkcji
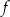 .
. -
Wyznacz zbiór wartości funkcji
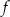 .
. -
Wyznacz zbiór wszystkich argumentów, dla których funkcja
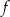 przyjmuje wartości ujemne.
przyjmuje wartości ujemne. -
Wyznacz zbiór wszystkich argumentów, dla których funkcja
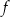 przyjmuje największą wartość.
przyjmuje największą wartość.
Miejscem zerowym funkcji liniowej 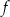 jest liczba 2, a punkt przecięcia wykresu funkcji
jest liczba 2, a punkt przecięcia wykresu funkcji 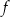 z osią
z osią 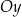 kartezjańskiego układu współrzędnych
kartezjańskiego układu współrzędnych 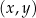 ma współrzędne
ma współrzędne 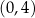 (zobacz rysunek).
(zobacz rysunek).
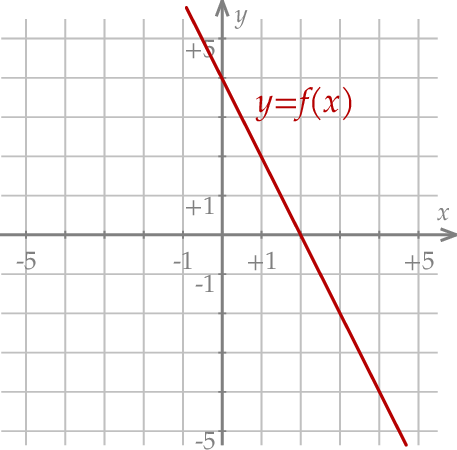
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Współczynnik kierunkowy prostej, która jest wykresem funkcji 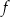 , jest równy , jest równy 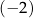 . . | P | F |
Pole trójkąta ograniczonego osiami kartezjańskiego układu współrzędnych 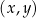 oraz wykresem funkcji oraz wykresem funkcji 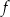 jest równe 8. jest równe 8. | P | F |
Informacja do zadań 12.1 – 12.3
W kartezjańskim układzie współrzędnych 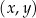 wykresem funkcji kwadratowej
wykresem funkcji kwadratowej 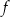 jest parabola, której wierzchołkiem jest punkt
jest parabola, której wierzchołkiem jest punkt 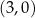 . Ta parabola przechodzi przez punkt o współrzędnych
. Ta parabola przechodzi przez punkt o współrzędnych 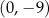 .
.
Funkcja 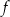 jest malejąca w przedziale
jest malejąca w przedziale
A) ![(− ∞ ,0]](https://img.zadania.info/zes/0091818/HzesT61x.png) B)
B) ![(− ∞ ,3]](https://img.zadania.info/zes/0091818/HzesT62x.png) C)
C) 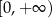 D)
D) 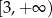
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych. Wzór funkcji 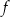 może być zapisany w postaci
może być zapisany w postaci
A) 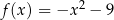 B)
B) 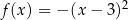 C)
C) 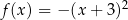
D) 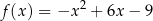 E)
E) 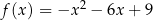 F)
F) 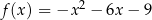
Funkcja kwadratowa 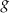 jest określona za pomocą funkcji
jest określona za pomocą funkcji 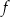 następująco:
następująco: 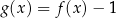 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja 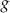 ma jedno miejsce zerowe. ma jedno miejsce zerowe. | P | F |
W kartezjańskim układzie współrzędnych 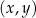 osią symetrii wykresu funkcji osią symetrii wykresu funkcji 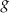 jest prosta o równaniu jest prosta o równaniu 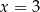 . . | P | F |
Funkcja logarytmiczna 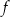 jest określona wzorem
jest określona wzorem 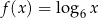 dla każdej dodatniej liczby rzeczywistej
dla każdej dodatniej liczby rzeczywistej  . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wartość funkcji 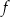 dla argumentu 36 jest równa 6. dla argumentu 36 jest równa 6. | P | F |
Funkcja 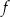 jest rosnąca. jest rosnąca. | P | F |
Ciąg 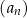 jest określony wzorem
jest określony wzorem 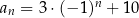 dla każdej liczby naturalnej
dla każdej liczby naturalnej 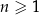 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Ciąg 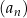 jest geometryczny. jest geometryczny. | P | F |
Suma ośmiu początkowych kolejnych wyrazów ciągu 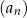 jest równa 80. jest równa 80. | P | F |
Trzywyrazowy ciąg 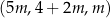 jest arytmetyczny, gdy liczba
jest arytmetyczny, gdy liczba 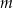 jest równa
jest równa
A) 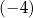 B)
B) 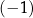 C) 1 D) 4
C) 1 D) 4
Dany jest ciąg geometryczny 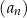 określony dla każdej liczby naturalnej
określony dla każdej liczby naturalnej 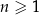 , w którym
, w którym 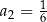 oraz
oraz 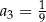 . Piąty wyraz ciągu
. Piąty wyraz ciągu 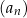 jest równy
jest równy
A) 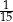 B)
B) 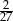 C)
C) 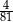 D)
D) 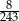
Informacja do zadań 17.1 i 17.2
Dany jest trójkąt prostokątny 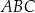 , w którym
, w którym 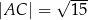 i
i 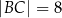 . Na przyprostokątnej
. Na przyprostokątnej 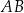 leży taki punkt
leży taki punkt 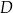 , że
, że 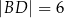 (zobacz rysunek).
(zobacz rysunek).

Sinus kąta ostrego 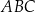 jest równy
jest równy
A) 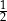 B)
B) 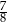 C)
C) 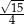 D)
D) 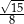
Tangens kąta ostrego 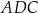 jest równy
jest równy
A) 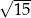 B)
B) 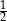 C)
C) 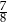 D)
D) 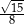
Kąt o mierze  jest rozwarty oraz
jest rozwarty oraz 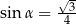 . Cosinus kąta o mierze
. Cosinus kąta o mierze  jest równy
jest równy
A) 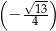 B)
B) 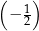 C)
C)  D)
D) 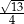
W trapezie prostokątnym 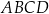 dłuższa podstawa
dłuższa podstawa 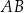 ma długość 7,5. Krótsza przekątna
ma długość 7,5. Krótsza przekątna 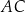 ma długość równą 6 i dzieli trapez na dwa trójkąty prostokątne (zobacz rysunek).
ma długość równą 6 i dzieli trapez na dwa trójkąty prostokątne (zobacz rysunek).
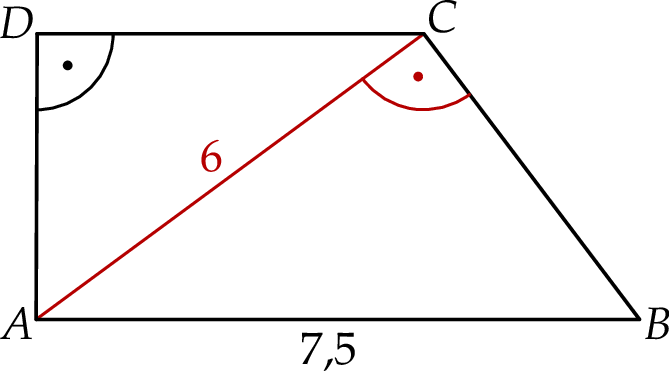
Oblicz pole trapezu 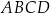 .
.
Dany jest okrąg o środku w punkcie 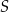 i promieniu 6. Miara kąta wpisanego
i promieniu 6. Miara kąta wpisanego 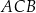 jest równa
jest równa 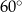 (zobacz rysunek).
(zobacz rysunek).

Długość łuku 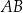 , na którym oparty jest kąt wpisany
, na którym oparty jest kąt wpisany 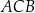 , jest równa
, jest równa
A)  B)
B) 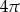 C)
C) 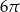 D)
D) 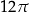
W kartezjańskim układzie współrzędnych 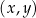 punkty
punkty 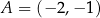 oraz
oraz 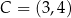 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 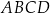 . Długość boku kwadratu
. Długość boku kwadratu 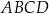 jest równa
jest równa
A) 5 B) 10 C) 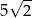 D)
D) 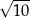
W kartezjańskim układzie współrzędnych 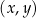 dana jest prosta
dana jest prosta 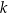 o równaniu
o równaniu 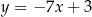 . Prosta
. Prosta 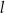 jest równoległa do prostej
jest równoległa do prostej 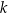 i przecina oś
i przecina oś 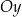 w punkcie
w punkcie 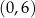 . Punkt o współrzędnych
. Punkt o współrzędnych 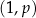 należy do prostej
należy do prostej 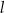 . Liczba
. Liczba 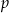 jest równa
jest równa
A) 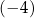 B)
B) 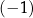 C)
C)  D) 7
D) 7
W kartezjańskim układzie współrzędnych 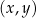 dane są cztery okręgi:
dane są cztery okręgi: 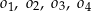 , o równaniach:
, o równaniach:
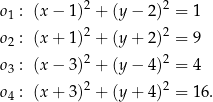
Okręgiem, który nie ma żadnego punktu wspólnego z osiami układu współrzędnych 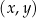 , jest
, jest
A) 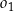 B)
B) 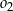 C)
C) 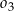 D)
D) 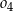
Podstawą ostrosłupa prawidłowego czworokątnego jest kwadrat o boku długości 4. Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod takim kątem  , że
, że 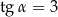 . Wysokość tego ostrosłupa jest równa
. Wysokość tego ostrosłupa jest równa
A) 3 B) 6 C) 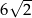 D) 12
D) 12
Długości trzech krawędzi wychodzących z jednego wierzchołka prostopadłościanu są trzema kolejnymi parzystymi liczbami naturalnymi. Najdłuższa krawędź tego prostopadłościanu ma długość 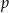 . Objętość tego prostopadłościanu jest równa
. Objętość tego prostopadłościanu jest równa
A) 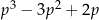 B)
B) 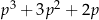
C) 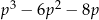 D)
D) 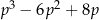
Objętość stożka o wysokości 2 jest równa 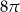 . Oblicz miarę kąta rozwarcia tego stożka.
. Oblicz miarę kąta rozwarcia tego stożka.
Wszystkich liczb naturalnych pięciocyfrowych nieparzystych, w których zapisie dziesiętnym występują wyłącznie cyfry 0, 1, 2, 3 (np. 12 303, 11 111), jest
A) 32 B) 384 C) 512 D) 576
Dane są dwa zbiory: 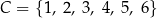 oraz
oraz 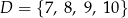 . Losujemy jedną liczbę ze zbioru
. Losujemy jedną liczbę ze zbioru 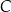 , a następnie losujemy jedną liczbę ze zbioru
, a następnie losujemy jedną liczbę ze zbioru 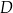 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 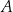 polegającego na tym, że wylosujemy liczby, których iloczyn będzie podzielny przez 4.
polegającego na tym, że wylosujemy liczby, których iloczyn będzie podzielny przez 4.
Do szkolnego koła czytelniczego należy 50 uczniów. Opiekun koła zebrał dane dotyczące liczby książek przeczytanych przez tych uczniów w listopadzie 2024 roku. W poniższej tabeli przedstawiono wyniki zebrane przez opiekuna.
| Liczba przeczytanych książek | 4 | 5 | 6 | 7 | 8 |
| Liczba uczniów, którzy przeczytali daną liczbę książek | 5 | 8 | 12 | 13 | 12 |
-
Oblicz średnią arytmetyczną liczby przeczytanych książek w tej grupie uczniów.
-
Oblicz medianę liczby przeczytanych książek w tej grupie uczniów.
Rozważamy wszystkie prostopadłościany 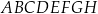 , w których krawędź
, w których krawędź 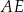 jest 3 razy dłuższa od krawędzi
jest 3 razy dłuższa od krawędzi 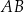 , a suma długości wszystkich dwunastu krawędzi prostopadłościanu jest równa 48 (zobacz rysunek).
, a suma długości wszystkich dwunastu krawędzi prostopadłościanu jest równa 48 (zobacz rysunek).
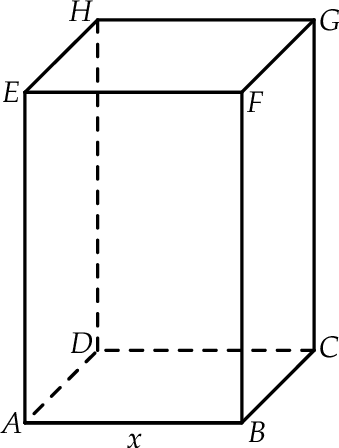
Niech 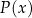 oznacza funkcję pola powierzchni całkowitej takiego prostopadłościanu w zależności od długości
oznacza funkcję pola powierzchni całkowitej takiego prostopadłościanu w zależności od długości  krawędzi
krawędzi 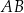 .
.
-
Wyznacz wzór i dziedzinę funkcji
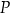 .
. -
Oblicz długość
 krawędzi
krawędzi 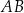 tego z rozważanych prostopadłościanów, którego pole powierzchni całkowitej jest największe.
tego z rozważanych prostopadłościanów, którego pole powierzchni całkowitej jest największe.

