/Szkoła średnia/Zadania maturalne/Matura 2025/Matura próbna/CKE, OKE, CEN
Próbny Egzamin Maturalny
z Matematyki (CKE)
poziom rozszerzony 12 grudnia 2024 Czas pracy: 180 minut
Ładunek elektryczny zgromadzony w kondensatorze można opisać zależnością
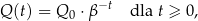
gdzie:
-
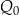 – ładunek elektryczny zgromadzony w kondensatorze w chwili początkowej (
– ładunek elektryczny zgromadzony w kondensatorze w chwili początkowej (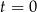 ) wyrażony w milikulombach
) wyrażony w milikulombach -
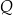 – ładunek elektryczny zgromadzony w kondensatorze w chwili
– ładunek elektryczny zgromadzony w kondensatorze w chwili 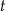 (licząc od chwili początkowej) wyrażony w milikulombach
(licząc od chwili początkowej) wyrażony w milikulombach -
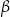 – stała dodatnia
– stała dodatnia -
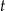 – czas wyrażony w sekundach.
– czas wyrażony w sekundach.
Wiadomo, że w chwili 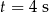 w kondensatorze był zgromadzony ładunek 2 milikulombów, a w chwili
w kondensatorze był zgromadzony ładunek 2 milikulombów, a w chwili 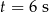 – ładunek 18 milikulombów. Oblicz, ile milikulombów ładunku było zgromadzone w tym kondensatorze w chwili
– ładunek 18 milikulombów. Oblicz, ile milikulombów ładunku było zgromadzone w tym kondensatorze w chwili 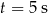 .
.
Okrąg  jest styczny do boków
jest styczny do boków 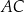 i
i 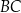 trójkąta
trójkąta 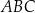 oraz przecina bok
oraz przecina bok 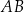 tego trójkąta w punktach
tego trójkąta w punktach 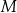 oraz
oraz 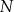 , przy czym
, przy czym 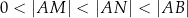 . Wykaż, że jeśli
. Wykaż, że jeśli 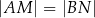 , to trójkąt
, to trójkąt 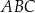 jest równoramienny.
jest równoramienny.
Iloczyn długości średnicy podstawy walca i wysokości walca jest równy 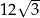 . Pole powierzchni całkowitej tego walca jest równe
. Pole powierzchni całkowitej tego walca jest równe 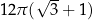 . Oblicz objętość tego walca.
. Oblicz objętość tego walca.
Wykaż, że
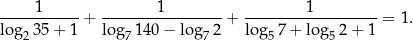
W pewnej lokalnej społeczności 35% osób ma wyższe wykształcenie. W tej społeczności językiem niemieckim dobrze włada 70% osób mających wyższe wykształcenie i 40% osób bez wyższego wykształcenia. Spośród członków tej społeczności wybieramy losowo jedną osobę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wybierzemy osobę z wyższym wykształceniem, jeżeli wiadomo, że ta osoba dobrze włada językiem niemieckim. Wynik zapisz w postaci ułamka dziesiętnego w zaokrągleniu do części setnych.
Rozwiąż równanie
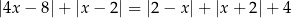
W kartezjańskim układzie współrzędnych 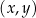 dane są: okrąg o równaniu
dane są: okrąg o równaniu 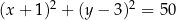 i punkty
i punkty 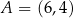 oraz
oraz 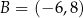 . Punkt
. Punkt 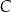 leży na tym okręgu i
leży na tym okręgu i 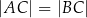 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 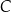 . Rozważ wszystkie przypadki.
. Rozważ wszystkie przypadki.
Oblicz granicę 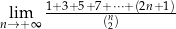 .
.
Rozwiąż równanie
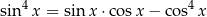
w zbiorze ![[− π,2 π]](https://img.zadania.info/zes/0095962/HzesT33x.png) .
.
Trzeci i piąty wyraz malejącego ciągu arytmetycznego 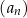 , określonego dla każdej liczby naturalnej
, określonego dla każdej liczby naturalnej 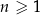 , spełniają warunek
, spełniają warunek 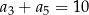 . Trzywyrazowy ciąg
. Trzywyrazowy ciąg 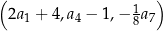 jest geometryczny. Oblicz wyrazy tego ciągu geometrycznego.
jest geometryczny. Oblicz wyrazy tego ciągu geometrycznego.
Funkcja kwadratowa 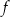 zmiennej rzeczywistej
zmiennej rzeczywistej  jest określona wzorem
jest określona wzorem
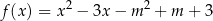
Wyznacz wszystkie wartości parametru 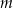 , dla których funkcja
, dla których funkcja 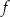 ma dwa różne miejsca zerowe
ma dwa różne miejsca zerowe 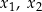 spełniające warunek
spełniające warunek 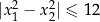 .
.
W trójkącie ostrokątnym 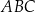 miara kąta
miara kąta 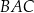 jest dwa razy większa od miary kąta
jest dwa razy większa od miary kąta 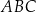 . Punkt
. Punkt 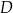 jest środkiem boku
jest środkiem boku 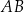 . Niech
. Niech  oznacza miarę kąta
oznacza miarę kąta 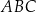 , natomiast
, natomiast 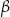 – miarę kąta
– miarę kąta 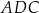 (zobacz rysunek).
(zobacz rysunek).
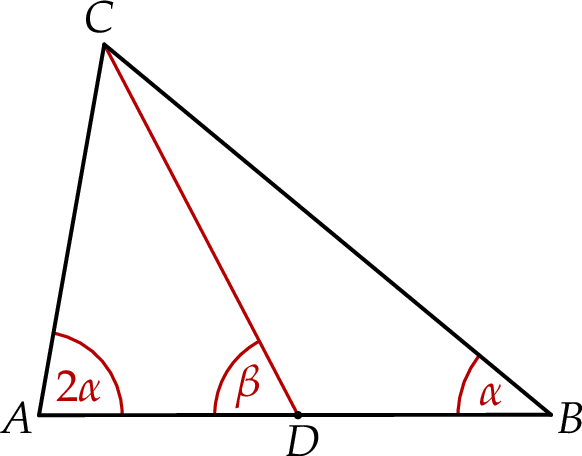
Oblicz 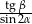 .
.
Funkcja 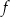 jest określona wzorem
jest określona wzorem 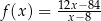 dla każdego
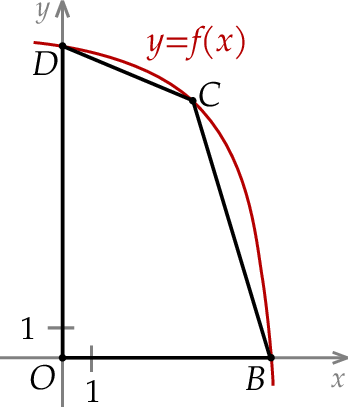
dla każdego 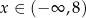 . W kartezjańskim układzie współrzędnych
. W kartezjańskim układzie współrzędnych 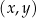 rozważamy wszystkie czworokąty
rozważamy wszystkie czworokąty 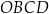 , w których:
, w których:
-
wierzchołek
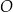 ma współrzędne
ma współrzędne 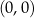 ;
; -
wierzchołki
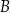 oraz
oraz 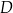 są punktami przecięcia wykresu funkcji
są punktami przecięcia wykresu funkcji 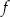 z osią – odpowiednio –
z osią – odpowiednio – 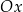 i
i 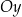 ;
; -
wierzchołek
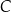 ma obie współrzędne dodatnie i leży na wykresie funkcji
ma obie współrzędne dodatnie i leży na wykresie funkcji 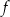 .
.
-
Wykaż, że pole
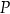 czworokąta
czworokąta 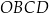 w zależności od pierwszej współrzędnej
w zależności od pierwszej współrzędnej  punktu
punktu 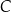 jest określone wzorem
jest określone wzorem 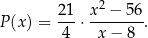
-
Oblicz współrzędne wierzchołka
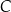 , dla których pole czworokąta
, dla których pole czworokąta 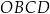 jest największe.
jest największe.

