/Szkoła średnia/Równania/Z wartością bezwględną/Kwadratowe/Z parametrem

Zadanie nr 2477760

Dla jakich wartości parametru 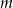m równanie 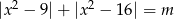2 2 |x − 9|+ |x − 1 6| = m ma dokładnie dwa różne pierwiastki.

Wersja PDF

Rozwiązanie

Zadanie najprościej jest rozwiązać posługując się wykresem. Aby narysować wykres prawej strony spróbujemy ją zapisać bez użycia wartości bezwzględnej. W zasadzie mamy 5 przypadków (odpowiadającym 4 miejscom zerowym wyrażeń pod wartością bezwzględną), ale niektóre z nich prowadzą do tego samego wzoru, więc je od razu połączymy (inny sposób zredukowania liczby przypadków – ponieważ funkcja jest parzysta, wystarczy wiedzieć jak wygląda dla 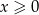x ≥ 0 ).

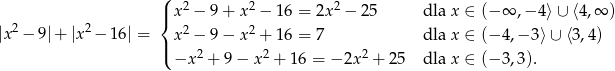
( |{ x2 − 9+ x2 − 16 = 2x 2 − 2 5 dla x ∈ (− ∞ ,− 4⟩∪ ⟨4,∞ ) |x2− 9|+ |x 2− 16| = x2 − 9− x2 + 16 = 7 dla x ∈ (− 4,− 3⟩∪ ⟨3,4 ) |( 2 2 2 −x + 9− x + 16 = − 2x + 25 dla x ∈ (− 3,3).

Możemy teraz narysować wykres tej funkcji (zielony wykres: 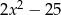2 2x − 25 , niebieski: 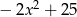2 − 2x + 2 5 , czerwony: lewa strona równania).

PIC

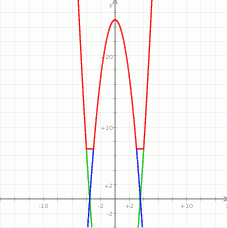
Widać teraz, że dokładnie dwa rozwiązania mamy dla 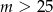m > 25 .  
Odpowiedź: m > 25

Wersja PDF