/Szkoła średnia/Równania/Z wartością bezwględną/Kwadratowe/Z parametrem

Zadanie nr 4990558

Naszkicuj wykres funkcji 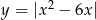2 y = |x − 6x | . Na podstawie wykresu określ dla jakich 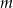m równanie 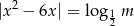|x2 − 6x | = log 1m 2 ma co najmniej 3 rozwiązania.

Wersja PDF

Rozwiązanie

Wykres podanej funkcji powstaje z wykresu funkcji

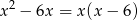
2 x − 6x = x(x − 6)

przez odbicie kawałka poniżej osi 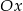Ox do góry. Powyższa funkcja kwadratowa ma wierzchołek dokładnie w środku pomiędzy pierwiastkami, czyli w punkcie

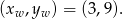
(xw ,yw ) = (3,9).

Teraz bez trudu rysujemy wykres.

PIC

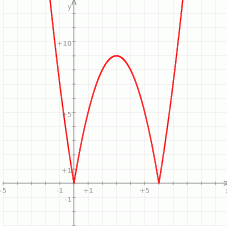
Z wykresu widać, że równanie 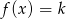f (x) = k ma co najmniej 3 rozwiązania dla 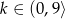k ∈ (0,9⟩ . Daje to nam (tu jest ważne, że funkcja 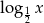log 1x 2 jest różnowartościowa)

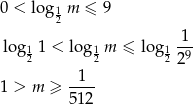
0 < log1 m ≤ 9 2 1-- log12 1 < log 12 m ≤ log12 29 1 1 > m ≥ ---- 512

 
Odpowiedź: m ∈ ⟨-1-,1) 512

Wersja PDF