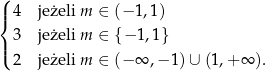/Szkoła średnia/Równania/Z wartością bezwględną/Kwadratowe/Z parametrem

Zadanie nr 9331862

Zbadaj liczbę rozwiązań równania 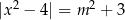2 2 |x − 4| = m + 3 w zależności od parametru m .

Wersja PDF

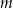Rozwiązanie

Sposób I

Najłatwiej jest myśleć, że z prawej strony mamy pewien parametr 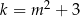2 k = m + 3 , który spełnia 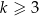k ≥ 3 . Lewą stronę łatwo narysować – jest to parabola 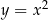y = x 2 przesunięta o 4 jednostki w dół (mamy 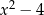x2 − 4 ) i część poniżej osi 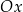Ox jest odbita do góry (mamy |x2 − 4| ).

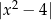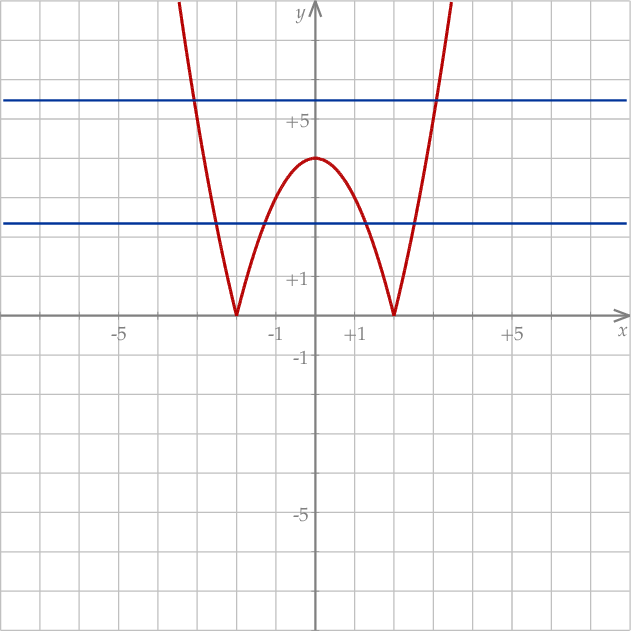
ZINFO-FIGURE

Gdy narysujemy ten wykres, staje się jasne, że ilość rozwiązań równania 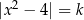|x2 − 4| = k wyraża się wzorem (pamiętamy, że k ≥ 3 !)

( |{ 4 je żeli 3 ≤ k < 4 |( 3 je żeli k = 4 2 je żeli k > 4.

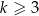Wracjąc do parametru 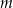m daje nam to

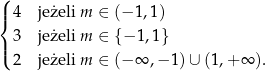
( |{ 4 je żeli m ∈ (− 1,1 ) 3 je żeli m ∈ { − 1,1} |( 2 je żeli m ∈ (− ∞ ,− 1) ∪ (1,+ ∞ ).

Sposób II

Tym razem rozważmy dwa przypadki.

Jeżeli 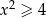x2 ≥ 4 to mamy równanie

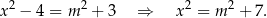
x2 − 4 = m 2 + 3 ⇒ x2 = m 2 + 7.

Widać, że to równanie ma zawsze dwa rozwiązania, ale interesuje nas kiedy spełniają one warunek x2 ≥ 4 . Sprawdzamy

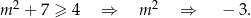
2 2 m + 7 ≥ 4 ⇒ m ⇒ − 3.

Nierówność ta jest zawsze spełniona, czyli zawsze mamy dwa pierwiastki spełniające 2 x ≥ 4 .

Teraz zajmijmy się przypadkiem 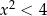x2 < 4 . Mamy wtedy równanie

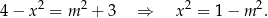
4− x 2 = m 2 + 3 ⇒ x2 = 1 − m 2.

Sprawdźmy, że rozwiązania tego równania (jeżeli są) spełniają nierówność 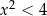x 2 < 4 :

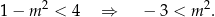
2 2 1 − m < 4 ⇒ − 3 < m .

Pozostało zatem ustalić ile jest tych rozwiązań. To jest jednak jasne:

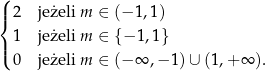
( |{ 2 je żeli m ∈ (− 1,1 ) 1 je żeli m ∈ { − 1,1} |( 0 je żeli m ∈ (− ∞ ,− 1) ∪ (1,+ ∞ ).

Dokładając dwa rozwiązania spełniające 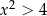2 x > 4 daje to nam tę samą odpowiedź, co poprzednio.  
Odpowiedź: Liczba rozwiązań: ( |{ 4 jeżeli m ∈ (− 1,1) 3 jeżeli m ∈ {− 1,1} |( 2 jeżeli m ∈ (− ∞ ,−1 )∪ (1,+ ∞ ).

Wersja PDF