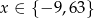Zadanie nr 2413577
Rozwiąż równanie 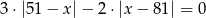 .
.
Rozwiązanie
Sposób I
Korzystamy z faktu, że
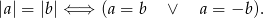
Przekształcamy dane równanie.
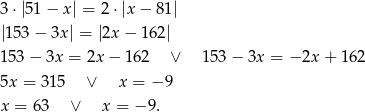
Sposób II
Dane równanie możemy zapisać w postaci
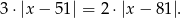
Tym razem rozpatrzymy trzy możliwe znaki wyrażeń w równaniu.
Jeżeli 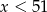 , to mamy równanie
, to mamy równanie
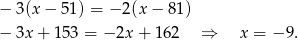
Jeżeli 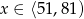 , to mamy równanie
, to mamy równanie
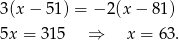
Jeżeli wreszcie 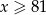 , to mamy dokładnie ten sam rachunek, co w pierwszym przypadku, czyli równanie jest w takiej sytuacji sprzeczne.
, to mamy dokładnie ten sam rachunek, co w pierwszym przypadku, czyli równanie jest w takiej sytuacji sprzeczne.
Odpowiedź: