/Szkoła średnia/Równania/Z wartością bezwględną/Liniowe

Zadanie nr 8485932

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 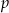p równanie 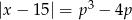3 |x− 15| = p − 4p ma dwa rozwiązania, których iloczyn jest liczbą dodatnią?

Rozwiązanie

Sposób I

Naszkicujmy wykres funkcji

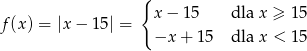
{ x − 15 dla x ≥ 1 5 f(x) = |x − 15 | = −x + 15 dla x < 15
PIC

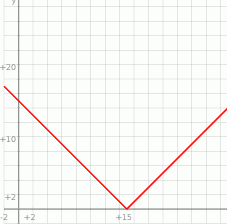
Z obrazka widać, że równanie 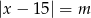|x− 15| = m ma dwa rozwiązania dla 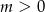m > 0 i zawsze jedno z nich jest dodatnie. Zatem iloczyn rozwiązań będzie dodatni, gdy drugie rozwiązanie też będzie dodatnie, czyli dla 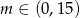m ∈ (0,15) . Musimy więc rozwiązać nierówność

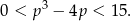
3 0 < p − 4p < 15.

Zajmijmy się najpierw lewą nierównością

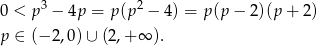
3 2 0 < p − 4p = p (p − 4) = p(p − 2 )(p + 2) p ∈ (− 2,0 )∪ (2,+ ∞ ).

Teraz prawa nierówność.

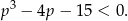
p 3 − 4p − 15 < 0.

Musimy rozłożyć lewą stronę na czynniki – aby to zrobić szukamy pierwiastków wymiernych wśród dzielników wyrazu wolnego. Sprawdzając po kolei można zauważyć, że pierwiastkiem jest 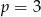p = 3 . Dzielimy więc lewą stronę przez 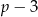p − 3 – my zrobimy to grupując wyrazy.

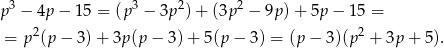
p3 − 4p − 15 = (p 3 − 3p 2)+ (3p2 − 9p) + 5p − 15 = 2 2 = p (p − 3) + 3p (p− 3)+ 5(p− 3) = (p − 3)(p + 3p + 5).

Trójmian w nawiasie nie ma pierwiastków (bo 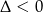Δ < 0 ), więc rozwiązaniem nierówności 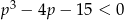p 3 − 4p − 15 < 0 jest przedział 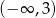(− ∞ ,3) . W połączeniu z rozwiązaniem poprzedniej nierówności otrzymujemy więc

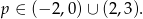
p ∈ (− 2,0 )∪ (2,3).

Sposób II

Równanie 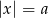|x | = a ma dwa rozwiązania wtedy i tylko wtedy, gdy 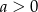a > 0 . W takim razie dane równanie będzie miało dwa rozwiązania tylko wtedy, gdy spełniona będzie nierówność.

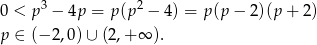
3 2 0 < p − 4p = p (p − 4) = p(p − 2 )(p + 2) p ∈ (− 2,0 )∪ (2,+ ∞ ).

Ponadto, łatwo wyznaczyć te rozwiązania

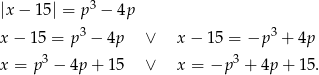
|x − 15| = p3 − 4p 3 3 x − 15 = p − 4p ∨ x − 15 = −p + 4p x = p3 − 4p + 15 ∨ x = −p 3 + 4p + 15.

Zauważmy, że ponieważ 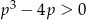3 p − 4p > 0 pierwszy z tych pierwiastków jest dodatni. To oznacza, że iloczyn pierwiastków będzie dodatni dokładnie wtedy, gdy drugi pierwiastek będzie dodatni. Mamy więc nierówność

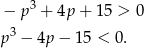
3 − p + 4p + 15 > 0 p3 − 4p − 1 5 < 0.

Nierówność tę rozwiązujemy dokładnie w ten sam sposób jak w sposobie I.  
Odpowiedź: p ∈ (−2 ,0)∪ (2,3)

Wersja PDF