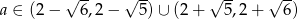/Szkoła średnia/Równania/Z wartością bezwględną/Liniowe

Zadanie nr 9877787

Dodaj do ulubionych
Dodaj do rozwiązanych

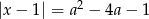Dla jakich wartości parametru a równanie 2 |x − 1| = a − 4a − 1 ma dwa dodatnie pierwiastki?

Rozwiązanie

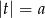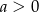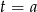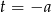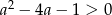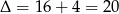Ogólnie równanie |t| = a ma dwa pierwiastki jeżeli a > 0 . W takim przypadku pierwiastki te są równe t = a i t = −a . Sprawdźmy więc na początek kiedy a2 − 4a − 1 > 0 (czyli kiedy podane równanie ma dwa pierwiastki). Liczymy, Δ = 16 + 4 = 2 0 ,

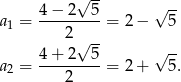
√ -- 4 − 2 5 √ -- a1 = ---------= 2− 5 2√ -- 4-+-2--5- √ -- a2 = 2 = 2+ 5.

A zatem

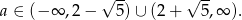
√ -- √ -- a ∈ (− ∞ ,2 − 5) ∪ (2+ 5,∞ ).

Przy powyższym założeniu pierwiastkami równania są liczby

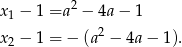
x 1 − 1 =a 2 − 4a − 1 2 x 2 − 1 = − (a − 4a− 1).

Przy naszym założeniu o dodatniości prawej strony równania, mamy 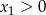x 1 > 0 . Pozstało sprawdzić kiedy x2 > 0 .

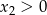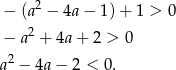
2 − (a − 4a− 1)+ 1 > 0 − a2 + 4a+ 2 > 0 2 a − 4a− 2 < 0.

Dalej, 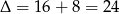Δ = 16 + 8 = 24

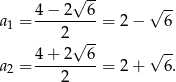
√ -- a = 4−--2--6-= 2 − √ 6- 1 2 4+ 2√ 6- √ -- a2 = ---------= 2 + 6. 2

Zatem

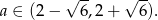
√ -- √ -- a ∈ (2 − 6,2 + 6).

W połączeniu z poprzednią nierównością mamy

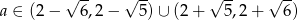
√ -- √ -- √ -- √ -- a ∈ (2− 6,2− 5)∪ (2 + 5,2 + 6)

 
Odpowiedź: √ -- √ -- √ -- √ -- a ∈ (2 − 6,2 − 5) ∪ (2+ 5,2+ 6)

Wersja PDF