/Szkoła średnia/Równania/Z wartością bezwględną/Liniowe

Zadanie nr 9983770

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 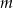m równanie 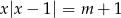x|x − 1| = m + 1 ma dwa różne rozwiązania?

Rozwiązanie

Zapiszmy lewą stronę bez wartości bezwględnej.

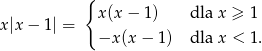
{ x|x − 1| = x (x − 1) dla x ≥ 1 −x (x − 1 ) dla x < 1.

Rysujemy wykres lewej strony i patrzymy ile ma punktów wspólnych z prostą 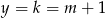y = k = m + 1 .

PIC

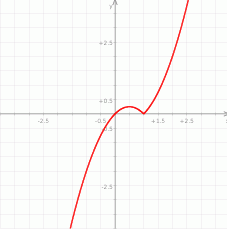
Pierwsza współrzędna wierzchołka paraboli 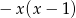− x(x − 1) jest dokładnie pomiędzy pierwiastkami, czyli 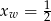xw = 12 . Mamy wtedy

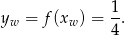
y = f (x ) = 1. w w 4

Zatem ilość rozwiązań równania 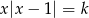x|x− 1| = k jest równa

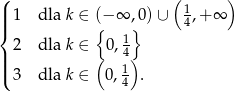
( ( ) ||| 1 dla k ∈ (− ∞ ,0)∪ 14,+ ∞ { { 1} | 2 dla k ∈ (0 ,4) ||( 1 3 dla k ∈ 0, 4 .

Wracając do parametru 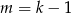m = k− 1 , liczba rozwiązań jest równa

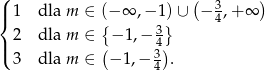
( ( ) |{ 1 dla m ∈ (− ∞ ,−1 )∪ − 34,+ ∞ 2 dla m ∈ {− 1,− 3} |( ( 4) 3 dla m ∈ − 1,− 34 .

 
Odpowiedź: m ∈ {− 1,− 3} 4

Wersja PDF