Zadanie nr 5459159
Dane są dwa okręgi o środkach w punktach 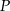 i
i 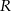 , styczne wewnętrznie w punkcie
, styczne wewnętrznie w punkcie 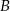 . Prosta
. Prosta 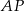 jest styczna do mniejszego okręgu w punkcie
jest styczna do mniejszego okręgu w punkcie 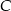 oraz
oraz 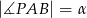 i
i 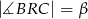 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 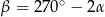 .
.
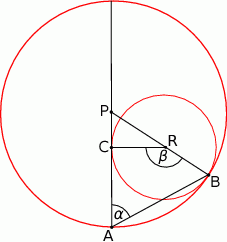
Rozwiązanie
Sposób I
Zauważmy, że trójkąt 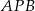 jest równoramienny (bo
jest równoramienny (bo 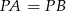 ). Zatem
). Zatem
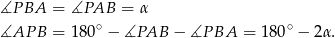
Patrzymy teraz na trójkąt prostokątny 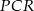 .
.
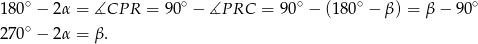
Sposób II
Jak poprzednio zauważamy, że trójkąt 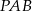 jest równoramienny oraz
jest równoramienny oraz 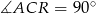 (kąt między styczną a promieniem poprowadzonym do punktu styczności). Korzystamy teraz z tego, że suma kątów w czworokącie
(kąt między styczną a promieniem poprowadzonym do punktu styczności). Korzystamy teraz z tego, że suma kątów w czworokącie 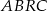 jest równa
jest równa 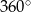 .
.