Zadanie nr 7173225
Dane są dwa okręgi o środkach w punktach 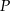 i
i 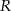 , styczne zewnętrznie w punkcie
, styczne zewnętrznie w punkcie 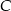 . Prosta
. Prosta 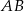 jest styczna do obu okręgów odpowiednio w punktach
jest styczna do obu okręgów odpowiednio w punktach 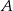 i
i 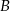 oraz
oraz 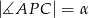 i
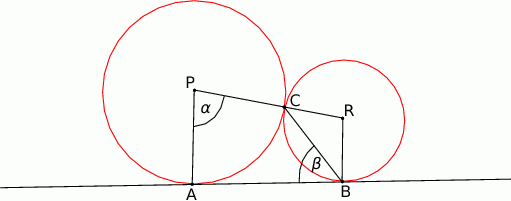
i 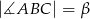 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 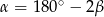 .
.
Rozwiązanie
Sposób I
Zauważmy, że promienie 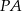 i
i 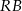 są prostopadłe do stycznej
są prostopadłe do stycznej 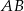 , więc dwa kąty czworokąta
, więc dwa kąty czworokąta 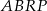 są proste. Suma kątów każdego czworokąta jest równa
są proste. Suma kątów każdego czworokąta jest równa 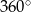 (bo można go podzielić na dwa trójkąty), więc
(bo można go podzielić na dwa trójkąty), więc
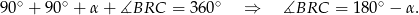
Trójkąt 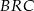 jest równoramienny, więc
jest równoramienny, więc
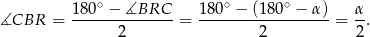
Mamy zatem
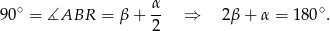
Sposób II
Trójkąt 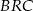 jest równoramienny, więc
jest równoramienny, więc
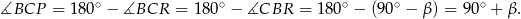
Korzystamy teraz z tego, że suma kątów w czworokącie 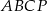 jest równa
jest równa 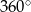 .
.