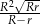/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Styczność/Dwa okręgi styczne

Zadanie nr 9319888

Dodaj do ulubionych
Dodaj do rozwiązanych

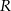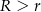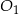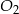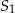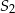Dane są 2 koła styczne zewnętrznie o promieniach R i r (R > r ) oraz środkach O 1 i O 2 . Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach S1 i S2 odpowiednio (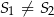S1 ⁄= S2 ). Oblicz pole trójkąta 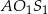AO S 1 1 , gdzie 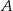A jest punktem przecięcia się prostych 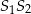S S 1 2 i O 1O 2 .

PIC

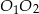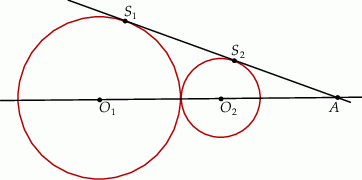
Rozwiązanie

Dorysujmy do podanego rysunku promienie okręgów oraz rzut 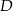D punktu 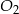O2 na prostą S 1O 1 .

PIC

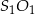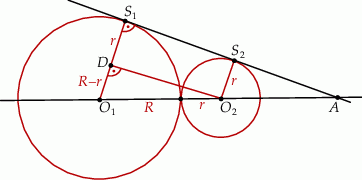
Obliczymy najpierw pole trójkąta 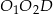O1O 2D (duży trójkąt jest do niego podobny w znanej skali, więc to nam wystarczy). Znamy jedną przyprostokątną oraz przeciwprostokątną tego trójkąta, możemy więc obliczyć drugą przyprostokątną.

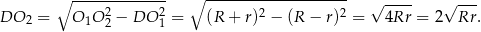
∘ ------------- ∘ -------------------- 2 2 2 2 √ ---- √ --- DO 2 = O 1O2 − DO 1 = (R + r) − (R − r) = 4Rr = 2 Rr .

Mamy zatem

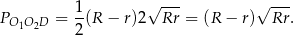
1 √ --- √ --- PO1O2D = -(R − r)2 Rr = (R − r) Rr . 2

Trójkąt 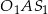O AS 1 1 jest podobny do trójkąta 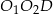O O D 1 2 w skali 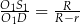O1S1= -R-- O1D R−r , zatem mamy

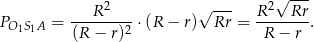
R 2 √ --- R2√Rr-- PO 1S1A = ---------⋅(R − r) Rr = -------. (R − r)2 R − r

 
Odpowiedź: 2√ -- RR-−Rrr

Wersja PDF