/Szkoła średnia/Funkcje/Sklejana z kilku funkcji

Zadanie nr 5721978

Dodaj do ulubionych
Dodaj do rozwiązanych

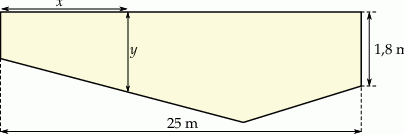
Basen ma długość 25 m. Przy głębszym z brzegów jego głębokość jest równa 1,8 m. Przekrój podłużny tego basenu przedstawiono poglądowo na rysunku. Głębokość 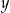y basenu zmienia się wraz z odległością x od brzegu w sposób opisany funkcją:

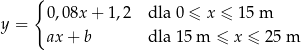
{ 0 ,08x + 1,2 dla 0 ≤ x ≤ 15 m y = ax + b dla 15 m ≤ x ≤ 25 m

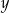Odległość x jest mierzona od płytszego brzegu w poziomie na powierzchni wody (zobacz rysunek). Wielkości x i y są wyrażone w metrach.

PIC

Oblicz wartość współczynnika a oraz wartość współczynnika 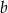b .

Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.