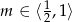/Szkoła średnia/Funkcje/Sklejana z kilku funkcji

Zadanie nr 9080793

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 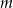m funkcja

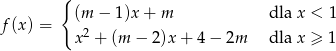
{ f(x) = (m − 1 )x+ m dla x < 1 x2 + (m − 2 )x+ 4− 2m dla x ≥ 1

przyjmuje tylko dodatnie wartości?

Rozwiązanie

Funkcja jest sklejona z dwóch funkcji, musimy zatem sprawdzić dla każdej z nich z osobna.

  • Sprawdzamy kiedy 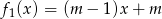f1(x ) = (m − 1 )x+ m jest dodatnie (przy założeniu 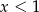x < 1 ). Wykres tej funkcji to prosta, jeżeli ma być ponad osią dla 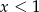x < 1 , to współczynnik kierunkowy musi być niedodatni oraz musi być 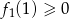f1(1) ≥ 0 . Daje to układ nierówności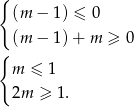
    { (m − 1) ≤ 0 (m − 1)+ m ≥ 0 { m ≤ 1 2m ≥ 1.

    Otrzymujemy stąd m ∈ ⟨1,1⟩ 2 .

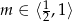  • Teraz sprawdzamy kiedy 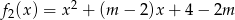f (x) = x 2 + (m − 2)x + 4 − 2m 2 jest powyżej osi. Aby to sprawdzić musimy wiedzieć, gdzie ta funkcja osiąga wartośc najmniejszą. Możliwości są dwie: albo w wierzchołku paraboli (jeżeli jest on w przedziale 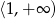⟨1,+ ∞ ) ) albo w punkcie 1 (jeżeli wierzchołek paraboli jest poza przedziałem 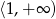⟨1,+ ∞ ) ). Sprawdzmy zatem, kiedy x ≥ 1 w .
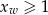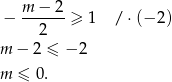
    m − 2 − ------≥ 1 / ⋅(− 2) 2 m − 2 ≤ − 2 m ≤ 0.

    Ale z poprzedniego podpunktu wiemy ,że 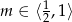1 m ∈ ⟨2,1 ⟩ , co oznacza, że wierzchołek paraboli jest zawsze poza przedziałem 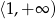⟨1 ,+ ∞ ) i funkcja 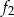f2 swoją najmniejszą wartość przyjmuje w punkcie 1. Pozostało zatem rozwiązać nierówność f2(1 ) > 0 .

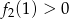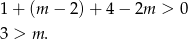
    1+ (m − 2) + 4 − 2m > 0 3 > m .

    co nie wnosi nic nowego do wcześniej uzyskanego warunku m ∈ ⟨12,1⟩ .

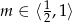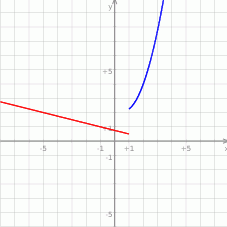
Dla ciekawskich, wykres funkcji dla przykładowej wartości 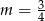m = 34 .  
Odpowiedź: m ∈ ⟨1,1⟩ 2

PIC
Wersja PDF