/Gimnazjum
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 8 kwietnia 2017 Czas pracy: 90 minut
Informacja do zadań 1 i 2
Ola odwiedziła koleżankę, a następnie wracała pieszo do domu. Na wykresie przedstawiono zależność między odległością Oli od domu a upływającym czasem.

Które z poniższych zdań jest fałszywe? Wybierz właściwą odpowiedź spośród podanych.
A) Ola dotarła do domu po 2,5 godziny.
B) Podczas powrotu do domu Ola zatrzymała się na półgodzinny postój.
C) W ciągu pierwszych dwóch godzin drogi powrotnej Ola przeszła 3 km.
D) O godzinie 12:15 Ola była w odległości 3 km od domu.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Średnia prędkość z jaką Ola wracała do domu wynosi 2,4 km/h | P | F |
| Średnia prędkość Oli w ciągu pierwszych 30 minut była mniejsza niż średnia prędkość w ciągu ostatnich 30 minut powrotu Oli do domu. | P | F |
Z cyfr 2, 1, 5 i 7 Przemek utworzył wszystkie możliwe liczby czterocyfrowe o różnych cyfrach. Które z poniższych zdań jest prawdziwe?
Wybierz właściwą odpowiedź spośród podanych.
A) Wszystkie liczby utworzone przez Przemka są mniejsze od 7519.
B) Wszystkie liczby utworzone przez Przemka są nieparzyste.
C) Dwie liczby utworzone przez Przemka są podzielne przez 18.
D) Wśród liczb utworzonych przez Przemka są liczby podzielne przez 4.
Wybierz odpowiedź spośród podanych.
Które z dwóch podanych liczb mają tę własność, że ich suma jest równa ich iloczynowi?
A)  i
i  B)
B) 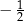 i 1. C)
i 1. C) 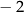 i
i 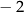 D)
D) 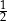 i
i 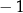
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba 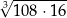 jest równa
jest równa
A) 12 B) 48 C) 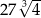 D)
D) 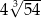
Jeśli 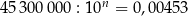 , to
, to  jest równe
jest równe
A) 9 B) 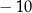 C) 10 D)
C) 10 D) 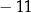
Dane są liczby  i
i 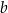 takie, że
takie, że 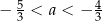 oraz
oraz 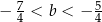 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Iloraz 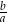 jest zawsze dodatni. jest zawsze dodatni. | P | F |
Różnica 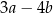 jest zawsze dodatnia. jest zawsze dodatnia. | P | F |
Pięć osób ze sprawdzianu otrzymało ocenę dopuszczającą, cztery dostateczną, trzy osoby ocenę bardzo dobrą, dwie celującą jedna niedostateczną i pięć osób ocenę dobrą.
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Mediana ocen z tego sprawdzianu jest równa
A) 3 B) 3,5 C) 4 D) 4,5
Cenę nart obniżono o 8%. Klient kupił narty po obniżonej cenie i dzięki temu zapłacił o 160 zł mniej, niż zapłaciłby przed obniżką.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Przed obniżką narty kosztowały
A) 2000 zł B) 1500 zł C) 1380 zł D) 960 zł
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
15 minut to 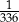 tygodnia. tygodnia. | P | F |
12 sekund to 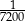 doby. doby. | P | F |
Na rysunku przedstawiono wykres pewnej funkcji 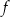 .
.
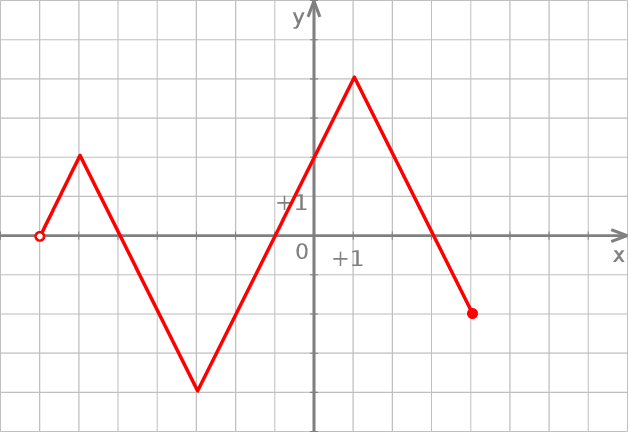
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Różnica między największą i najmniejszą wartością funkcji jest równa 8. | P | F |
Do wykresu funkcji należy punkt 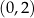 . . | P | F |
Na siatce kwadratowej narysowano czworokąt. Bok kwadratu siatki jest równy 1.
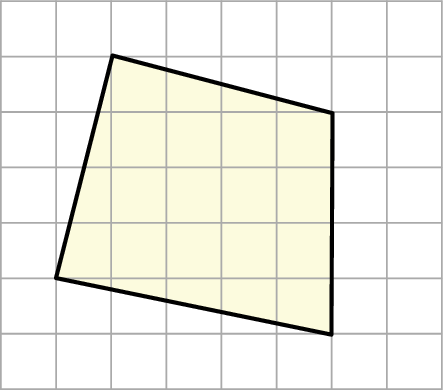
Dokończ zdanie, wybierając odpowiedź spośród podanych.
Pole narysowanego czworokąta jest równe
A) 18,5 B) 20 C) 21 D) 22
Ola ma 7 lat. Średnia arytmetyczna wieku Ewy i Karola jest równa 10 lat.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Średnia arytmetyczna wieku Oli, Ewy i Karola jest równa
A) 6 lat B) 9 lat C) 10 lat D) 15 lat
Tomek otrzymał torebkę, w której było  cukierków. Sam zjadł z tej torebki 8 cukierków, a pozostałe cukierki rozdzielił pomiędzy swoich 5 kolegów. Czworo z tych chłopców otrzymało tyle samo cukierków, a piąty z nich, Szymon, otrzymał o jeden cukierek więcej od pozostałych. Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Liczba cukierków, które otrzymał Szymon jest równa
cukierków. Sam zjadł z tej torebki 8 cukierków, a pozostałe cukierki rozdzielił pomiędzy swoich 5 kolegów. Czworo z tych chłopców otrzymało tyle samo cukierków, a piąty z nich, Szymon, otrzymał o jeden cukierek więcej od pozostałych. Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Liczba cukierków, które otrzymał Szymon jest równa
A) 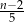 B)
B) 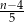 C)
C) 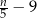 D)
D) 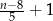
Doświadczenie losowe polega na czterokrotnym rzucie symetryczną monetą.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Jeśli w pierwszych trzech rzutach wypadnie orzeł, to w czwartym rzucie
A) jest bardziej prawdopodobne, że wypadnie reszka.
B) na pewno wypadnie reszka.
C) jest tak samo prawdopodobne, że wypadnie orzeł lub reszka.
D) jest bardziej prawdopodobne, że wypadnie orzeł.
Okrąg wpisany w czworokąt 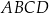 ma środek
ma środek 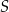 i jest styczny do boków
i jest styczny do boków 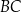 i
i 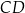 odpowiednio w punktach
odpowiednio w punktach 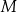 i
i 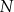 . Kąt
. Kąt 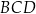 ma miarę
ma miarę 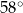 (rysunek).
(rysunek).
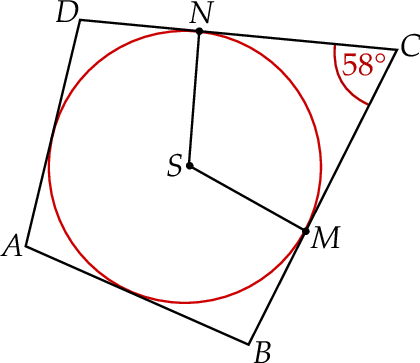
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Kąt 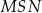 ma miarę
ma miarę
A) 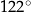 B)
B) 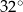 C)
C) 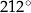 D)
D) 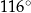
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Figurą, która ma oś symetrii, ale nie ma środka symetrii jest
A) równoległobok B) prostokąt C) trójkąt równoboczny D) romb
Ewa narysowała kwadrat o boku 1, prostokąt o bokach 3 i 1 oraz kąt prosty o wierzchołku 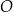 .
.
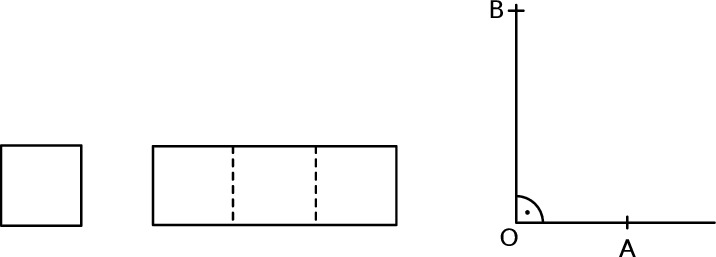
Następnie od wierzchołka 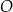 kąta prostego odmierzyła na jednym ramieniu kąta odcinek
kąta prostego odmierzyła na jednym ramieniu kąta odcinek 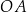 o długości równej przekątnej kwadratu, a na drugim ramieniu – odcinek
o długości równej przekątnej kwadratu, a na drugim ramieniu – odcinek 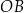 o długości równej przekątnej prostokąta.
o długości równej przekątnej prostokąta.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość odcinka 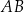 jest równa
jest równa
A) 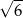 B)
B) 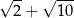 C)
C) 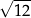 D)
D) 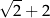
Na rysunku poniżej przedstawiono siatkę pewnej bryły. Punkty: 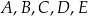 są środkami jej krawędzi.
są środkami jej krawędzi.
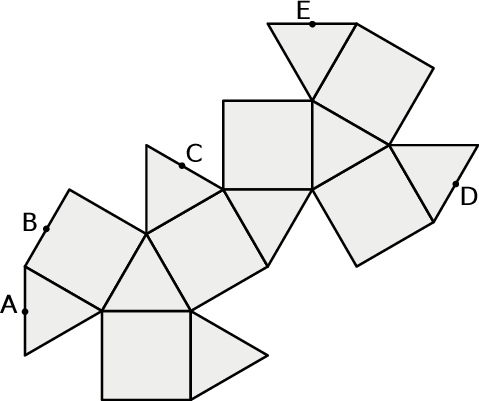
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Po złożeniu bryły z tej siatki punkt 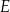 pokryje się z punktem
pokryje się z punktem
A) 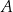 B)
B) 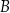 C)
C) 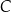 D)
D) 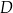
Objętość metalowej kuli jest równa 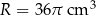 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość tej kuli jest większa niż 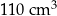 . . | P | F |
Pole powierzchni tej kuli jest równe 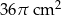 . . | P | F |
Janek i Ludwik mają razem 54 lata. Trzynaście lat temu Ludwik był 3 razy starszy od Janka. Ile lat temu Ludwik był dwa razy starszy od Janka?
Uczniowie klas pierwszych pewnego gimnazjum pojechali na wycieczkę pociągiem. W każdym zajętym przez nich przedziale było sześcioro uczniów. Jeśli w każdym przedziale byłoby ośmioro uczniów, to zajęliby oni o 2 przedziały mniej. Ilu uczniów pojechało na tę wycieczkę? Zapisz obliczenia.
Do pojemnika w kształcie stożka wlano 1 litr wody, która wypełniła to naczynie do 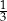 wysokości. Jaka jest całkowita pojemność tego naczynia?
wysokości. Jaka jest całkowita pojemność tego naczynia?