/Gimnazjum
Egzamin gimnazjalny
z Matematyki 20 kwietnia 2017 Czas pracy: 90 minut
Turysta  szedł ze schroniska w kierunku szczytu, natomiast turysta
szedł ze schroniska w kierunku szczytu, natomiast turysta  schodził ze szczytu w kierunku schroniska. Obaj szli tym samym szlakiem i tego samego dnia. Wykresy przedstawiają, na jakiej wysokości względem poziomu morza znajdowali się turyści w określonym czasie.
schodził ze szczytu w kierunku schroniska. Obaj szli tym samym szlakiem i tego samego dnia. Wykresy przedstawiają, na jakiej wysokości względem poziomu morza znajdowali się turyści w określonym czasie.
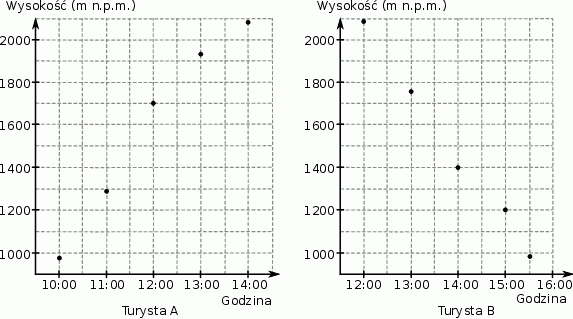
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Turyści spotkali się na szlaku między godziną 13:00 a 14:00. | P | F |
| Turyści spotkali się w miejscu położonym między 1700 a 2000 m n.p.m. | P | F |
Paweł przejechał na rowerze trasę długości 700 m w czasie 2 min.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Prędkość średnia, jaką uzyskał Paweł na tej trasie, jest równa
A) 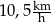 B)
B) 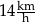 C)
C) 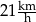 D)
D) 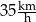
Dane są cztery wyrażenia:
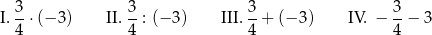
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Największą wartość ma wyrażenie
A) I B) II C) III D) IV
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zaokrąglenie ułamka okresowego 9,2(6) z dokładnością do 0,001 jest równe
A) 9,262 B) 9,263 C) 9,266 D) 9,267
Dana jest liczba dwucyfrowa. W tej liczbie cyfrą dziesiątek jest  , cyfrą jedności jest
, cyfrą jedności jest 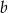 oraz spełnione są warunki:
oraz spełnione są warunki: 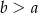 i
i 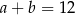 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Warunki zadania spełnia siedem liczb. | P | F |
| Wszystkie liczby spełniające warunki zadania są podzielne przez 3. | P | F |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 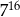 jest 7 razy większa od liczby jest 7 razy większa od liczby 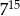 . . | P | F |
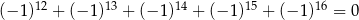 | P | F |
Dane są trzy wyrażenia:
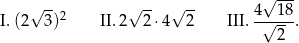
Wartości których wyrażeń są mniejsze od 15? Wybierz właściwą odpowiedź spośród podanych.
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) I, II i III.
W pewnej szkole do egzaminu gimnazjalnego przystąpiło o 60 chłopców więcej niż dziewcząt. Chłopcy stanowili 65% liczby osób piszących egzamin. Ile dziewcząt przystąpiło do tego egzaminu? Wybierz właściwą odpowiedź spośród podanych.
A) 200 B) 130 C) 70 D) 39
Dane są dwie liczby  i
i 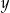 . Wiadomo, że
. Wiadomo, że 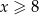 oraz
oraz 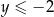 .
.
![]()
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Najmniejsza możliwa wartość różnicy 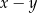 jest równa:
jest równa:
A) 10 B) 6 C) 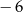 D)
D) 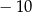
Na rysunku przedstawiono sposób ułożenia wzoru z jednakowych elementów i podano długości dwóch fragmentów tego wzoru.
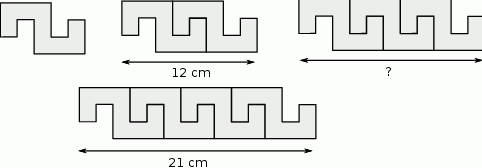
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Fragment wzoru złożony z 3 elementów ma długość
A) 15 cm B) 15,75 cm C) 16,5 cm D) 18 cm
Do dwóch koszy wrzucono piłki szare i czarne. Na diagramie przedstawiono liczbę piłek każdego koloru w I i w II koszu.
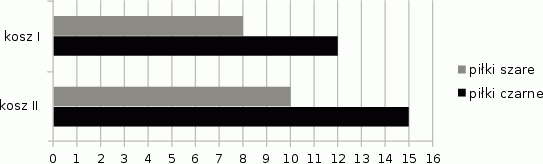
Czy wylosowanie piłki czarnej z kosza II jest bardziej prawdopodobne niż wylosowanie piłki czarnej z kosza I? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A. | w koszu II jest więcej piłek czarnych niż w koszu I. |
| B. | stosunek liczby piłek czarnych do liczby wszystkich piłek jest taki sam w obu koszach. |
| C. | w koszu II jest o 3 piłki czarne więcej niż w koszu I, ale szarych – tylko o 2 więcej. |
Uczniowie mieli wyznaczyć zmienną  ze wzoru
ze wzoru 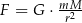 . W tabeli przedstawiono rezultaty pracy kilkorga z nich.
. W tabeli przedstawiono rezultaty pracy kilkorga z nich.
| Uczeń | Agata | Bartek | Czarek | Dorota |
| Rezultat | 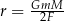 | 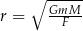 | 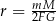 | 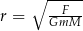 |
Kto z uczniów poprawnie wyznaczył zmienną  ? Wybierz właściwą odpowiedź spośród podanych.
? Wybierz właściwą odpowiedź spośród podanych.
A) Agata B) Bartek C) Czarek D) Dorota
Sprzedawca kupił do swojego sklepu 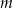 kilogramów marchwi i
kilogramów marchwi i 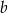 kilogramów buraków: zapłacił po 1,50 zł za kilogram marchwi i po 0,90 zł za kilogram buraków. Warzywa te sprzedał za łączną kwotę 180 złotych. Które wyrażenie przedstawia różnicę kwoty uzyskanej za sprzedane warzywa i kosztu ich zakupu? Wybierz właściwą odpowiedź spośród podanych.
kilogramów buraków: zapłacił po 1,50 zł za kilogram marchwi i po 0,90 zł za kilogram buraków. Warzywa te sprzedał za łączną kwotę 180 złotych. Które wyrażenie przedstawia różnicę kwoty uzyskanej za sprzedane warzywa i kosztu ich zakupu? Wybierz właściwą odpowiedź spośród podanych.
A) 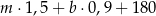 B)
B) 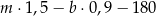
C) 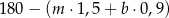 D)
D) 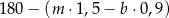
Dwie przecinające się proste utworzyły cztery kąty. Suma miar trzech z tych kątów jest równa 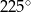 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Suma miar kątów ostrych wyznaczonych przez te proste jest równa 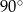 . . | P | F |
| Jeden z dwóch kątów przyległych jest trzy razy większy od drugiego kąta. | P | F |
Z kartki w kształcie kwadratu o boku 6 odcięto ćwierć koła o promieniu 6 (patrz rysunek).
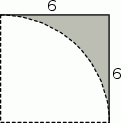
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Pole powierzchni pozostałej zacieniowanej części kartki jest równe
A) 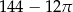 B)
B) 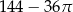 C)
C) 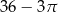 D)
D) 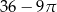
Z kwadratu odcięto trójkąty tak, że linie cięcia przeprowadzono przez środki boków tego kwadratu (rysunek I). Z odciętych trójkątów ułożono trójkąt 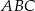 (rysunek II).
(rysunek II).
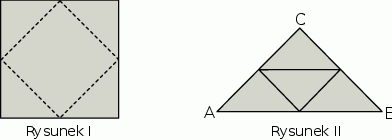
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 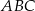 jest prostokątny i równoramienny. jest prostokątny i równoramienny. | P | F |
Pole trójkąta 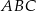 jest połową pola kwadratu. jest połową pola kwadratu. | P | F |
W okręgu o środku 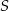 zaznaczono kąt oparty na łuku
zaznaczono kąt oparty na łuku 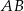 . Przez punkt
. Przez punkt  poprowadzono prostą
poprowadzono prostą  styczną do okręgu.
styczną do okręgu.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Zaznaczony na rysunku kąt  zawarty między styczną
zawarty między styczną 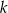 i cięciwą
i cięciwą 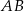 ma miarę
ma miarę
A) 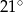 B)
B) 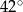 C)
C) 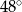 D)
D) 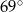
Prostokąt o wymiarach 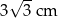 i
i 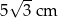 podzielono na 15 jednakowych kwadratów.
podzielono na 15 jednakowych kwadratów.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole jednego kwadratu jest równe
A) 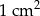 B)
B) 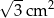 C)
C) 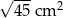 D)
D) 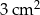
Do akwarium w kształcie prostopadłościanu o wymiarach 90 cm, 40 cm, 50 cm wlano 40 litrów wody. Ile litrów wody należy jeszcze dolać do akwarium, aby sięgała ona do połowy jego wysokości? Wybierz właściwą odpowiedź spośród podanych.
A) 50 B) 70 C) 90 D) 140
Jacek z 14 jednakowych sześciennych kostek skleił figurę, której widok z przodu i z tyłu przedstawiono na rysunkach.

Całą figurę, również od spodu, Jacek pomalował. Ile sześciennych kostek ma pomalowane dokładnie 4 ściany? Wybierz właściwą odpowiedź spośród podanych.
A) 8 B) 7 C) 6 D) 5
Zapisano trzy różne liczby, których średnia arytmetyczna jest równa 4, oraz dwie inne liczby, których średnia arytmetyczna jest równa 2. Uzasadnij, że średnia arytmetyczna zestawu tych pięciu liczb jest równa 3,2. Zapisz obliczenia.
Do przewiezienia 27 ton żwiru potrzeba 5 małych i 2 dużych ciężarówek albo 3 małych i 3 dużych ciężarówek (przy wykorzystaniu całkowitej ich ładowności). Ile co najmniej kursów musi wykonać jedna duża ciężarówka, aby przewieźć 27 ton żwiru? Zapisz obliczenia.
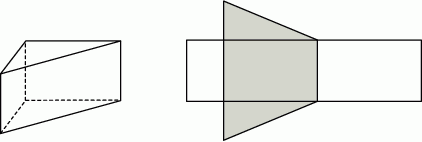
Na rysunku przedstawiono graniastosłup prosty o podstawie trójkąta prostokątnego i jego siatkę. Dwie dłuższe krawędzie podstawy graniastosłupa mają 12 cm i 13 cm długości, a pole zacieniowanej części siatki graniastosłupa jest równe 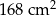 . Oblicz objętość tego graniastosłupa. Zapisz obliczenia.
. Oblicz objętość tego graniastosłupa. Zapisz obliczenia.