/Gimnazjum
Egzamin Gimnazjalny
z Matematyki 19 kwietnia 2016 Czas pracy: 90 minut
Zastęp harcerzy wyruszył z przystanku autobusowego do obozowiska. Na wykresie przedstawiono zależność między odległością harcerzy od obozowiska a czasem wędrówki.
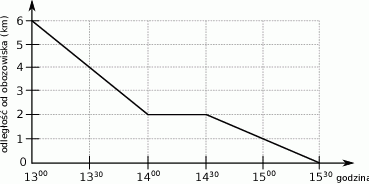
Które z poniższych zdań jest fałszywe? Wybierz właściwą odpowiedź spośród podanych.
A) Harcerze dotarli do obozowiska po 2,5 godziny.
B) W ciągu pierwszej godziny harcerze przeszli 2 km.
C) Podczas wędrówki harcerze zatrzymali się na 30-minutowy postój.
D) O godzinie 14:15 harcerze byli w odległości 2 km od obozowiska.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Odległość między punktami, które na osi liczbowej odpowiadają liczbom 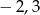 i
i 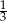 jest równa
jest równa
A) 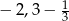 B)
B) 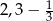 C)
C) 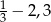 D)
D) 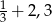
Z cyfr 2, 3 i 5 Ania utworzyła wszystkie możliwe liczby trzycyfrowe o różnych cyfrach. Które z poniższych zdań jest prawdziwe?
Wybierz właściwą odpowiedź spośród podanych.
A) Wszystkie liczby utworzone przez Anię są nieparzyste.
B) Wszystkie liczby utworzone przez Anię są mniejsze od 530.
C) Dwie liczby utworzone przez Anię są podzielne przez 5.
D) Wśród liczb utworzonych przez Anię są liczby podzielne przez 3.
Dane są liczby

Która z tych liczb jest największa? Wybierz właściwą odpowiedź spośród podanych.
A) I B) II C) III D) IV
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba 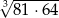 jest równa
jest równa
A) 72 B) 36 C) 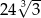 D)
D) 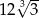
W tabeli podano, w jaki sposób zmienia się cena biletu na prom w ciągu całego roku.
| Cena podstawowa biletu na prom | 40 zł |
| Cena biletu w sezonie zimowym | cena podstawowa obniżona o 20% |
| Cena biletu w sezonie letnim | cena podstawowa podwyższona o 200% |
| Cena biletu poza sezonem zimowym i letnim | cena podstawowa |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Bilet na prom w sezonie letnim jest droższy od biletu w sezonie zimowym o
A) 88 zł B) 72 zł C) 48 zł D) 32 zł
Dane są liczby  i
i 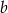 takie, że
takie, że 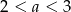 oraz
oraz 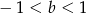 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Iloraz 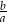 jest zawsze dodatni. jest zawsze dodatni. | P | F |
Różnica 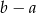 jest zawsze dodatnia. jest zawsze dodatnia. | P | F |
W klasie IIIa liczba dziewcząt stanowi  liczby wszystkich uczniów tej klasy.
liczby wszystkich uczniów tej klasy.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
W klasie IIIa
A) jest więcej chłopców niż dziewcząt.
B) liczba dziewcząt stanowi  liczby chłopców.
liczby chłopców.
C) jest dwa razy więcej dziewcząt niż chłopców.
D) stosunek liczby chłopców do liczby dziewcząt jest równy 1:3.
Cenę roweru obniżono o 8%. Klient kupił rower po obniżonej cenie i dzięki temu zapłacił o 120 zł mniej, niż zapłaciłby przed obniżką.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Przed obniżką ten rower kosztował
A) 2000 zł B) 1500 zł C) 1380 zł D) 960 zł
W pewnym zakładzie każdy z pracowników codziennie maluje taką samą liczbę jednakowych ozdób. Pracownicy potrzebowali 12 dni roboczych, aby wykonać zamówienie. Gdyby było ich o dwóch więcej, to czas wykonania tego zamówienia byłby o 3 dni krótszy.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczbę pracowników  tego zakładu można obliczyć, rozwiązując równanie
tego zakładu można obliczyć, rozwiązując równanie
A) 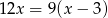 B)
B) 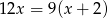 C)
C) 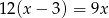 D)
D) 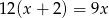
Na rysunku przedstawiono wykres pewnej funkcji.
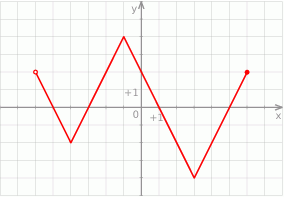
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Funkcja przyjmuje wartość największą dla argumentu 4. | P | F |
| Funkcja przyjmuje wartość 0 dla czterech argumentów. | P | F |
W układzie współrzędnych narysowano sześciokąt foremny o boku 2 tak, że jednym z jego wierzchołków jest punkt 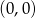 , a jeden z jego boków leży na osi
, a jeden z jego boków leży na osi  (rysunek).
(rysunek).
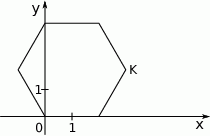
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Współrzędne wierzchołka K tego sześciokąta są równe
A) 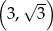 B)
B) 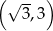 C)
C) 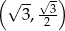 D)
D) 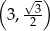
W układzie współrzędnych narysowano sześciokąt foremny o boku 2 tak, że jednym z jego wierzchołków jest punkt 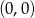 , a jeden z jego boków leży na osi
, a jeden z jego boków leży na osi  . Do tego sześciokąta dorysowujemy kolejne takie same sześciokąty. Umieszczamy je tak, jak na rysunku, aby każdy następny sześciokąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego sześciokąta leżał na osi
. Do tego sześciokąta dorysowujemy kolejne takie same sześciokąty. Umieszczamy je tak, jak na rysunku, aby każdy następny sześciokąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego sześciokąta leżał na osi  . Poniżej przedstawiono dorysowane, zgodnie z tą regułą, sześciokąty, które ponumerowano kolejnymi liczbami naturalnymi.
. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, sześciokąty, które ponumerowano kolejnymi liczbami naturalnymi.
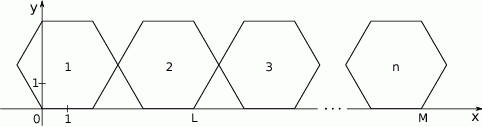
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pierwsza współrzędna wierzchołka 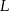 w drugim sześciokącie jest równa 6. w drugim sześciokącie jest równa 6. | P | F |
Pierwsza współrzędna wierzchołka 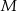 w w  –tym sześciokącie jest równa –tym sześciokącie jest równa 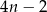 . . | P | F |
Kasia ma 6 lat. Średnia arytmetyczna wieku Ani i Pawła jest równa 12 lat.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Średnia arytmetyczna wieku Kasi, Ani i Pawła jest równa
A) 6 lat B) 9 lat C) 10 lat D) 15 lat
Na rysunku przedstawiono siatkę nietypowej sześciennej kostki do gry. Rzucamy jeden raz taką kostką.
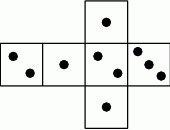
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyrzucenia nieparzystej liczby oczek jest 2 razy większe niż prawdopodobieństwo wyrzucenia parzystej liczby oczek. | P | F |
Prawdopodobieństwo wyrzucenia liczby oczek mniejszej od 3 jest równe  . . | P | F |
Proste 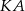 i
i 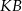 są styczne do okręgu o środku
są styczne do okręgu o środku 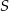 w punktach
w punktach 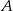 i
i 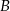 , a kąt
, a kąt 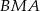 ma miarę
ma miarę 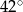 (rysunek).
(rysunek).
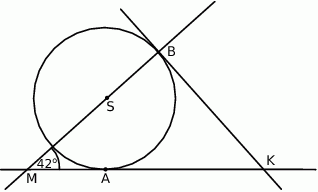
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Kąt 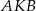 jest równy
jest równy
A) 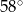 B)
B) 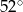 C)
C) 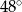 D)
D) 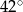
Punkty 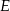 i
i 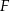 są środkami boków
są środkami boków 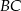 i
i 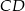 kwadratu
kwadratu 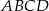 (rysunek).
(rysunek).
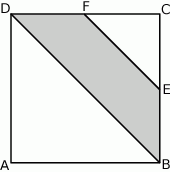
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 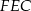 stanowi stanowi  pola kwadratu pola kwadratu 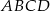 . . | P | F |
Pole czworokąta 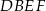 stanowi stanowi  pola kwadratu pola kwadratu 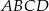 . . | P | F |
Ewa narysowała kwadrat o boku 1, prostokąt o bokach 2 i 1 oraz kąt prosty o wierzchołku 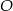 .
.
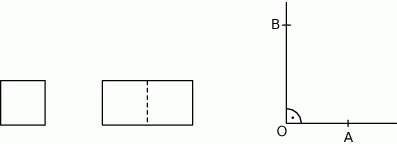
Następnie od wierzchołka 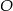 kąta prostego odmierzyła na jednym ramieniu kąta odcinek
kąta prostego odmierzyła na jednym ramieniu kąta odcinek 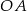 o długości równej przekątnej kwadratu, a na drugim ramieniu – odcinek
o długości równej przekątnej kwadratu, a na drugim ramieniu – odcinek 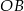 o długości równej przekątnej prostokąta.
o długości równej przekątnej prostokąta.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość odcinka 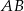 jest równa
jest równa
A) 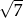 B)
B) 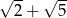 C)
C) 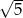 D)
D) 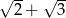
Każdy bok kwadratu 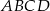 podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano ośmiokąt (rysunek).
podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano ośmiokąt (rysunek).
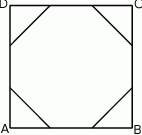
Które z poniższych zdań jest prawdziwe? Wybierz właściwą odpowiedź spośród podanych.
A) Ośmiokąt jest foremny.
B) Wszystkie boki ośmiokąta mają taką samą długość.
C) Każdy kąt wewnętrzny ośmiokąta ma miarę 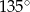 .
.
D) Obwód ośmiokąta jest większy od obwodu kwadratu 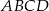 .
.
Na rysunku poniżej przedstawiono siatkę sześcianu. Punkty: 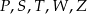 są środkami jego krawędzi.
są środkami jego krawędzi.
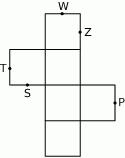
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Po złożeniu sześcianu z tej siatki punkt 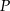 pokryje się z punktem
pokryje się z punktem
A) 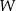 B)
B) 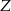 C)
C) 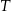 D)
D) 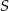
Jedenaście piłeczek, ponumerowanych kolejnymi liczbami naturalnymi od 1 do 11, wrzucono do pudełka. Janek, nie patrząc na piłeczki, wyjmuje je z pudełka. Ile najmniej piłeczek musi wyjąć Janek, aby mieć pewność, że przynajmniej jedna wyjęta piłeczka jest oznaczona liczbą parzystą? Odpowiedź uzasadnij.
Uczniowie klas trzecich pewnego gimnazjum pojechali na wycieczkę pociągiem. W każdym zajętym przez nich przedziale było ośmioro uczniów. Jeśli w każdym przedziale byłoby sześcioro uczniów, to zajęliby oni o 3 przedziały więcej. Ilu uczniów pojechało na tę wycieczkę? Zapisz obliczenia.
Pojemnik z kremem ma kształt walca o promieniu podstawy 4 cm i wysokości 4,5 cm. Po jego otwarciu okazało się, że krem wypełnia tylko wyżłobioną w pojemniku półkulę o promieniu 3 cm. Ile razy objętość tej półkuli jest mniejsza od objętości walca? Zapisz obliczenia.