/Gimnazjum
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 2 kwietnia 2016 Czas pracy: 90 minut
Informacja do zadań 1 i 2
Pomiędzy dworcem kolejowym i lotniskiem kursują pociągi według schematu przedstawionego na rysunku. Pociągi te poruszają się ze średnią prędkością 72 km/h.
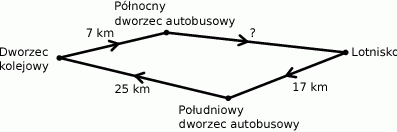
Jak długo trwa przejazd pociągu jadącego z lotniska do dworca kolejowego? Wybierz właściwą odpowiedź spośród podanych.
A) 40 minut B) 36 minut C) 30 minut D) 35 minut
Z północnego dworca autobusowego pociąg wyjeżdża o godz. 14:23, a godz. 14:33 wyjeżdża drugi pociąg z lotniska. Oba pociągi w tym samym czasie dojeżdżają do swoich kolejnych stacji, tzn. pierwszy pociąg do lotniska, a drugi pociąg do południowego dworca autobusowego.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Odległość między północnym dworcem autobusowym i lotniskiem jest równa
A) 30 km B) 29 km C) 32 km D) 28 km
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczba 16 razy większa od 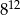 jest równa
jest równa
A) 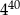 B)
B) 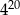 C)
C) 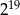 D)
D) 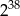
Dane jest przybliżenie 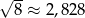 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
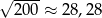 | P | F |
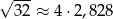 | P | F |
Jacek ma o 4 lata młodszego brata Kamila, który ma  lat. Kamil ma koleżankę Basię, która jest od niego dwa razy starsza. Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Różnica wieku Basi i Jacka jest równa
lat. Kamil ma koleżankę Basię, która jest od niego dwa razy starsza. Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Różnica wieku Basi i Jacka jest równa
A) 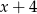 B)
B) 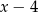 C)
C)  D)
D) 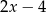
W dodatniej liczbie trzycyfrowej cyfra dziesiątek jest średnią arytmetyczną jej pozostałych dwóch cyfr, a iloczyn cyfr setek i jedności jest równy 12. Ile jest liczb spełniających te warunki? Wybierz właściwą odpowiedź spośród podanych.
A) Jedna. B) Dwie. C) Trzy. D) Cztery.
Do 200 ml soku dolano 0,3 litra wody. Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Stężenie soku w otrzymanym napoju jest równe
A) 66% B) 40% C) 150% D) 60%
Na wykresie przedstawiono, jak zmienia się masa porcji lodów z wafelkiem w zależności od liczby gałek lodów.
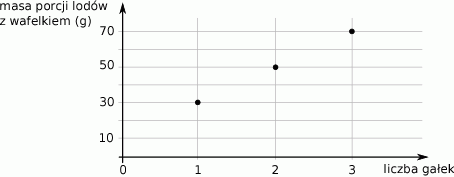
Jaką masę ma wafelek? Wybierz właściwą odpowiedź spośród podanych.
A) 10 g B) 20 g C) 30 g D) 40 g
Rozwiązaniem układu równań 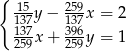 jest para liczb
jest para liczb
A) 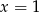 i
i 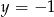 B)
B) 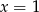 i
i 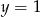 C)
C) 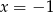 i
i 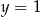 D)
D) 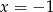 i
i 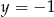
Doświadczenie losowe polega na trzykrotnym rzucie monetą. Jeśli wypadnie orzeł, zapisujemy 5, a jeśli reszka – zapisujemy 4. Wynikiem doświadczenia jest zapisana liczba trzycyfrowa. Jakie jest prawdopodobieństwo, że zapisana liczba jest podzielna przez 6? Wybierz właściwą odpowiedź spośród podanych.
A) 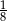 B)
B) 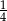 C)
C)  D)
D) 
Narysowana poniżej figura składa się z dwóch kwadratów o boku 2 i dwóch ćwiartek koła.
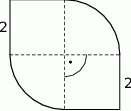
Obwód tej figury jest równy
A) 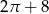 B)
B) 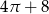 C)
C) 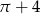 D)
D) 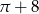
Liczba  jest ujemna, a liczba
jest ujemna, a liczba 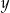 jest dodatnia.
jest dodatnia.
Ile spośród liczb: 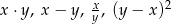 jest ujemnych? Wybierz właściwą odpowiedź spośród podanych.
jest ujemnych? Wybierz właściwą odpowiedź spośród podanych.
A) Jedna. B) Dwie. C) Trzy. D) Cztery.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Liczba osi symetrii figury przedstawionej na rysunku jest równa
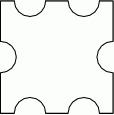
A) 1 B) 2 C) 3 D) 4
Informacja do zadań 14 i 15
Jeżeli 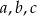 i
i 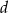 są długościami kolejnych boków czworokąta, to przekątne tego czworokąta są prostopadłe wtedy i tylko wtedy, gdy
są długościami kolejnych boków czworokąta, to przekątne tego czworokąta są prostopadłe wtedy i tylko wtedy, gdy 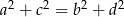 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Czworokąt, którego dwa przeciwległe boki mają długości 7 i 24, a dwa pozostałe boki mają długości 15 i 20 ma prostopadłe przekątne. | P | F |
Czworokąt, w którym długości kolejnych boków są równe: 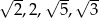 ma prostopadłe przekątne. ma prostopadłe przekątne. | P | F |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Jeżeli trzy kolejne boki czworokąta mają długości: 5, 6, 7 oraz przekątne tego czworokąta są prostopadłe, to czwarty bok tego czworokąta ma długość
A) 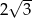 B)
B) 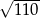 C)
C) 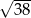 D)
D) 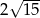
Na rysunku przedstawiono sześciokąt foremny o boku równym 4 cm. Przekątna 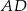 dzieli go na dwa przystające trapezy równoramienne.
dzieli go na dwa przystające trapezy równoramienne.
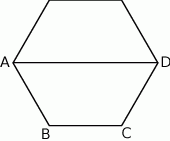
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Pole trapezu 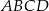 jest równe
jest równe
A) 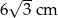 B)
B) 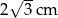 C)
C) 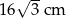 D)
D) 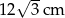
Jeżeli odcinek 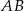 przecina oś
przecina oś 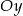 układu współrzędnych, to końce tego odcinka mogą mieć współrzędne
układu współrzędnych, to końce tego odcinka mogą mieć współrzędne
Wybierz odpowiedź spośród podanych
A) 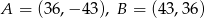
B) 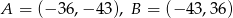
C) 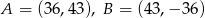
D) 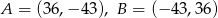
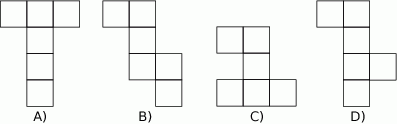
Który z poniższych rysunków nie może być siatką sześcianu? Wybierz odpowiedź spośród podanych.
Mediana zestawu liczb 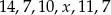 jest 9.
jest 9.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Liczba  jest równa
jest równa
A) 2 B) 9 C) 8 D) 10
Na rysunku przedstawiono sześcian i ostrosłup prawidłowy czworokątny. Bryły mają jednakowe podstawy i równe wysokości, a różnica objętości tych brył jest równa 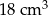 .
.
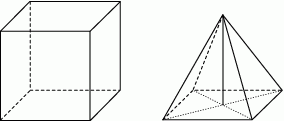
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Objętość ostrosłupa jest sześć razy mniejsza od objętości sześcianu. | P | F |
| Wysokość ostrosłupa ma długość 6 cm. | P | F |
Znajdź liczbę dwucyfrową wiedząc, że różnica między cyfrą dziesiątek, a cyfrą jedności tej liczby jest równa 3, oraz suma tej liczby i liczby powstałej przez zamianę miejscami jej cyfr jest równa 77.
Kąt przy podstawie trójkąta równoramiennego 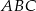 ma miarę
ma miarę 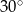 . Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta
. Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta 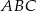 .
.
Przekrój betonowego kanału melioracyjnego ma kształt trapezu o podstawach 0,5 m i 1,5 m.
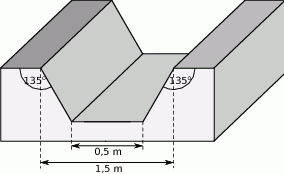
Oblicz ile wody zmieści się w takim kanale, jeżeli jego długość jest równa 50 m.

