/Gimnazjum
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 7 kwietnia 2018 Czas pracy: 90 minut
Informacja do zadań 1 i 2
W budynku przeprowadzono test dwóch zainstalowanych w nim wind. W czasie procedury testowej każda z wind co 5 minut zatrzymywała się na jednym z pięter. Wykresy przedstawiają położenie każdej z wind w trakcie 70 minutowej procedury testowej.
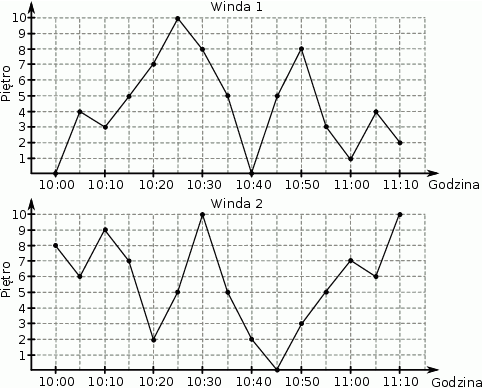
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W trakcie testu windy czterokrotnie znalazły się na tej samej wysokości. | P | F |
| Windy dwa razy zatrzymały się w tym samym czasie na tym samym piętrze. | P | F |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Maksymalna prędkość względna, z jaką poruszały się w stosunku do siebie windy, jest równa
A) 5 piętr na minutę B) 1,4 piętra na minutę C) 10 pięter na minutę D) 2 piętra na minutę
Dane są cztery wyrażenia:
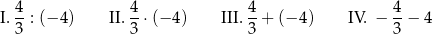
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Największą wartość ma wyrażenie
A) I B) II C) III D) IV
Dana jest funkcja określona wzorem 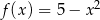 , gdzie
, gdzie  jest liczbą rzeczywistą.
jest liczbą rzeczywistą.
Zaznacz P, jeśli zdanie jest prawdziwe, lub zaznacz F – jeśli jest fałszywe.
Dla argumentu 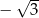 funkcja funkcja 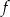 przyjmuje wartość 8. przyjmuje wartość 8. | P | F |
| Są dwa różne argumenty, dla których funkcja przyjmuje wartość 3. | P | F |
Dana jest liczba trzycyfrowa. W tej liczbie cyfrą setek jest  , cyfrą dziesiątek jest
, cyfrą dziesiątek jest 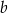 , cyfrą jedności jest
, cyfrą jedności jest  oraz spełnione są warunki:
oraz spełnione są warunki: 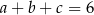 ,
, 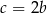 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Warunki zadania spełniają dwie liczby. | P | F |
| Wszystkie liczby spełniające warunki zadania są podzielne przez 24. | P | F |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 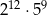 ma 10 cyfr. ma 10 cyfr. | P | F |
Suma cyfr liczby 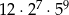 jest równa 3. jest równa 3. | P | F |
Dane są trzy wyrażenia:
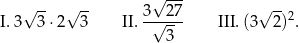
Wartości których wyrażeń są większe od 6? Wybierz właściwą odpowiedź spośród podanych.
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) I, II i III.
Dane są dwie liczby  i
i 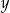 . Wiadomo, że
. Wiadomo, że 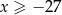 oraz
oraz 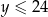 .
.
![]()
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Największa możliwa wartość różnicy 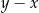 jest równa:
jest równa:
A) 0 B) 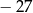 C) 51 D) 24
C) 51 D) 24
Informacja do zadań 9 i 10
Na rysunku przedstawiono schemat budowy muru z cegieł oraz dwa przykładowe mury: jeden o szerokości 5 i wysokości 3 cegieł oraz drugi o szerokości 6 i wysokości 5 cegieł.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli zwiększamy szerokość muru dwukrotnie, to liczba cegieł potrzebnych do jego budowy również rośnie dwukrotnie. | P | F |
| W każdym ze zbudowanych w ten sposób murów liczba cegieł jest liczbą parzystą. | P | F |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Do zbudowania muru o szerokości  i wysokości 11 cegieł potrzeba
i wysokości 11 cegieł potrzeba
A) 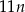 cegieł. B)
cegieł. B) 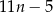 cegieł. C)
cegieł. C) 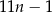 cegieł. D)
cegieł. D) 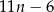 cegieł.
cegieł.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Pary liczb 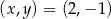 i
i 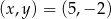 należą do zbioru rozwiązań układu równań
należą do zbioru rozwiązań układu równań
A) 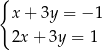 B)
B) 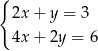 C)
C) 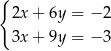 D)
D) 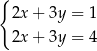
W dwóch koszach umieszczono koszulki niebieskie i czerwone. Na diagramie przedstawiono liczbę koszulek każdego koloru w I i w II koszu.
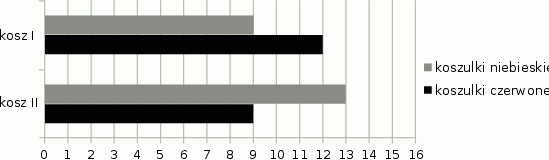
Czy wylosowanie niebieskiej koszulki z kosza I jest bardziej prawdopodobne niż wylosowanie czerwonej koszulki z kosza II? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | w koszu I jest tyle samo koszulek niebieskich ile jest koszulek czerwonych w koszu II. |
| B) | stosunek liczby koszulek niebieskich do liczby koszulek czerwonych w I koszu jest taki sam jak stosunek liczby koszulek czerwonych do liczby koszulek niebieskich w II koszu. |
| C) | w koszu II jest więcej koszulek niebieskich niż jest koszulek czerwonych w pierwszym koszu. |
Właściciel sklepu przemysłowego kupił  opakowań 5-kilogramowego proszku do prania w cenie
opakowań 5-kilogramowego proszku do prania w cenie  złotych za kilogram. Zakupiony proszek sprzedał za łączną kwotę 3200 zł. Od uzyskanego przychodu, czyli od różnicy między kwotą uzyskaną ze sprzedaży i kosztami zakupu musi zapłacić podatek dochodowy w wysokości 19%. Które wyrażenie przedstawia wysokość podatku jaki musi zapłacić właściciel tego sklepu? Wybierz właściwą odpowiedź spośród podanych.
złotych za kilogram. Zakupiony proszek sprzedał za łączną kwotę 3200 zł. Od uzyskanego przychodu, czyli od różnicy między kwotą uzyskaną ze sprzedaży i kosztami zakupu musi zapłacić podatek dochodowy w wysokości 19%. Które wyrażenie przedstawia wysokość podatku jaki musi zapłacić właściciel tego sklepu? Wybierz właściwą odpowiedź spośród podanych.
A) 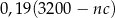 B)
B) 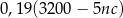
C) 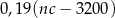 D)
D) 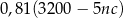
Przekątne trapezu równoramiennego przecinają się pod kątem 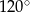 i dzielą się w stosunku 2:1. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
i dzielą się w stosunku 2:1. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeden z kątów trapezu ma miarę 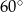 . . | P | F |
| Przekątna dzieli jeden z kątów trapezu w stosunku 3:1. | P | F |
W kwadracie o boku 6 narysowano dwie ćwiartki okręgu o promieniu 6 (patrz rysunek).
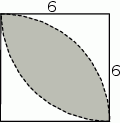
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole zacieniowanej figury jest równe 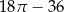 | P | F |
| Obwód zacieniowanej figury jest mniejszy od 21. | P | F |
Na boku 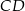 prostokąta
prostokąta 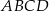 o bokach długości 12 cm i 20 cm wybrano punkt
o bokach długości 12 cm i 20 cm wybrano punkt 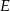 w ten sposób, że pole czworokąta
w ten sposób, że pole czworokąta 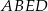 jest równe
jest równe 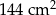 .
.
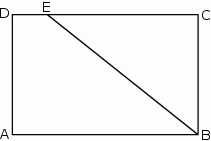
Dokończ zdanie. Zaznacz dobrą odpowiedź.
Długość odcinka 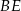 jest równa
jest równa
A) 20 B) 24 C) 18 D) 16
W restauracji znajdują się dwa akwaria w kształcie prostopadłościanów. Większe z nich ma wymiary 120 cm, 80 cm, 100 cm. Mniejsze akwarium napełniono wodą do połowy jego wysokości, a następnie przelano tę wodę do większego akwarium i przelana woda wypełniła 25% objętości większego akwarium. Jaka jest objętość mniejszego akwarium? Wybierz właściwą odpowiedź spośród podanych.
A) 480 B) 240 C) 120 D) 360
W sześciokącie foremnym 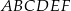 poprowadzono trzy przekątne i otrzymano trójkąt
poprowadzono trzy przekątne i otrzymano trójkąt 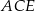 .
.
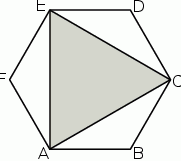
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Obwód trójkąta 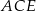 jest większy niż jest większy niż  obwodu sześciokąta obwodu sześciokąta 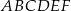 . . | P | F |
Pole trójkąta 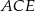 stanowi połowę pola sześciokąta stanowi połowę pola sześciokąta 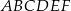 . . | P | F |
W okręgu o środku 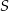 zaznaczono kąt oparty na łuku
zaznaczono kąt oparty na łuku 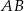 . Przez punkt
. Przez punkt 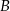 poprowadzono prostą
poprowadzono prostą  styczną do okręgu.
styczną do okręgu.
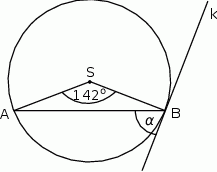
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Zaznaczony na rysunku kąt  zawarty między styczną
zawarty między styczną 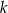 i cięciwą
i cięciwą 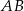 ma miarę
ma miarę
A) 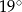 B)
B) 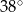 C)
C) 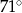 D)
D) 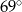
Z przedstawionych na rysunku siatek sklejono cztery sześciany.

W ilu z tych sześcianów naprzeciwko ściany oznaczonej literą 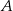 znajduje się ściana oznaczona literą
znajduje się ściana oznaczona literą 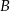 ? Wybierz właściwą odpowiedź spośród podanych.
? Wybierz właściwą odpowiedź spośród podanych.
A) 1 B) 2 C) 3 D) 4
Wykaż, że jeżeli 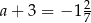 i
i 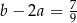 , to wartość wyrażenia
, to wartość wyrażenia 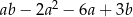 jest równa
jest równa 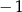 .
.
Grupa motocyklistów w ciągu czterech dni pokonała dystans 221 km, przy czym liczby pokonanych kilometrów w kolejnych dniach są do siebie w proporcji 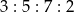 . Oblicz ile kilometrów motocykliści pokonywali w kolejnych dniach.
. Oblicz ile kilometrów motocykliści pokonywali w kolejnych dniach.
Obwód rombu wynosi 68 cm, a długość jednej z jego przekątnych stanowi 187,5% długości drugiej przekątnej. Oblicz pole tego rombu.
Na rysunku przedstawiono graniastosłup prosty o podstawie trójkąta prostokątnego i jego siatkę. Najkrótsza krawędź podstawy graniastosłupa ma długość 9 cm, a wysokość graniastosłupa ma długość 8 cm. Pole zacieniowanej części siatki graniastosłupa jest równe 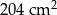 . Oblicz pole powierzchni całkowitej tego graniastosłupa. Zapisz obliczenia.
. Oblicz pole powierzchni całkowitej tego graniastosłupa. Zapisz obliczenia.


