/Gimnazjum
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 6 kwietnia 2019 Czas pracy: 90 minut
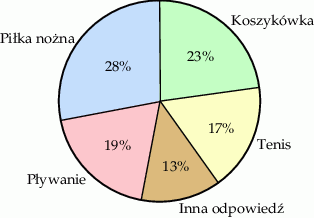
Grupie dwustu osób zadano pytanie: „Jaka jest twoja ulubiona dyscyplina sportu?”. Wyniki tej ankiety przedstawiono na wykresie.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Z informacji podanych na diagramie wynika, że:
A) 28 osób jako ulubioną dyscyplinę podało piłkę nożną.
B) Łączna liczba odpowiedzi: „piłka nożna” i „tenis” jest równa liczbie wszystkich pozostałych odpowiedzi.
C) Liczba odpowiedzi „pływanie” była o 4 większa od liczby odpowiedzi „tenis”.
D) Liczba odpowiedzi „tenis” była o 6 mniejsza od liczby odpowiedzi „koszykówka”.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Na osi liczbowej narysowano odcinek, którego końcami są największa i najmniejsza spośród liczb 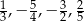 . Długość tego odcinka jest równa
. Długość tego odcinka jest równa
A) 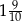 B)
B) 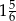 C)
C) 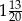 D)
D) 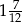
Korzystając z tego, że 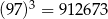 , wskaż wartość liczby
, wskaż wartość liczby 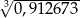 .
.
Zaznacz dobrą odpowiedź.
A) 0,0097 B) 0,097 C) 0,97 D) 9,7
Samolot pasażerski spala średnio 10 ton paliwa w ciągu godziny lotu.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W ciągu minuty lotu samolot spala ponad 200 kg paliwa. | P | F |
| Spalenie przez samolot 1800 kg paliwa trwa krócej niż 12 minut. | P | F |
Jacek i Ewa mieli w maju odpowiednio 1200 i 2000 złotych oszczędności. W czerwcu oszczędności Jacka wzrosły o 25%, ale w sumie mieli z Ewą nadal tyle samo oszczędności co w maju.
O ile procent zmalały w czerwcu oszczędności Ewy? Wybierz odpowiedź spośród podanych.
A) 15% B) 17,6% C) 25% D) 30%
Danych jest pięć liczb
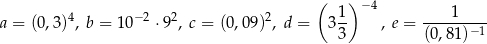
Która równość jest fałszywa? Wybierz odpowiedź spośród podanych.
A) 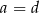 B)
B) 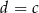 C)
C) 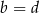 D)
D) 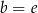 E)
E) 
Marcel narysował prostokąt położony w układzie współrzędnych tak jak na pierwszym rysunku. Kolejne przystające do niego prostokąty rysował w taki sposób, że kolejny rysowany prostokąt był obrócony o 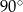 oraz lewy dolny wierzchołek tego prostokąta był prawym górnym wierzchołkiem poprzedniego prostokąta (rysunek 2.).
oraz lewy dolny wierzchołek tego prostokąta był prawym górnym wierzchołkiem poprzedniego prostokąta (rysunek 2.).
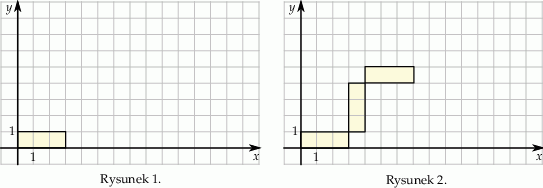
Oceń prawdziwość podanych zdań.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli punkt
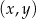 jest prawym górnym wierzchołkiem 20 prostokąta to
jest prawym górnym wierzchołkiem 20 prostokąta to 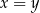 | P | F |
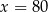 | P | F |
Na diagramie zaznaczono, w których miesiącach urodzili się uczniowie klasy IIa.
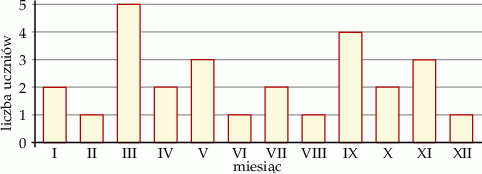
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Z informacji podanych na diagramie wynika, że
A) klasa IIa liczy 28 uczniów.
B) najwięcej uczniów urodziło się w kwietniu.
C) większość uczniów urodziła się w pierwszej połowie roku.
D) liczba uczniów urodzonych w maju jest większa niż łączna liczba uczniów urodzonych w lipcu i w sierpniu.
Na rysunku przedstawiono wykres pewnej funkcji.
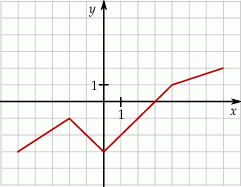
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja przyjmuje wartość 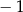 dla argumentu dla argumentu 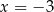 . . | P | F |
Dla wszystkich argumentów 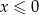 funkcja przyjmuje wartości ujemne. funkcja przyjmuje wartości ujemne. | P | F |
Pan Tadeusz postanowił pomalować ściany w swoim mieszkaniu. Łączna powierzchnia ścian, które postanowił pomalować jest równa 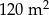 . Pod uwagę wziął dwa rodzaje farb.
. Pod uwagę wziął dwa rodzaje farb.
| Rodzaj farby | Wydajność | Cena |
| Fabra lateksowa | 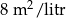 | 5 zł za 1 litr |
| Farba akrylowa | 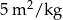 | 3 zł za 1 kg |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Koszt pomalowania 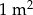 ściany jest niższy w przypadku farby akrylowej, niż w przypadku farby lateksowej. ściany jest niższy w przypadku farby akrylowej, niż w przypadku farby lateksowej. | P | F |
| Kupując tańszą farbę, pan Tadeusz zaoszczędzi 5 zł. | P | F |
Od kartonika w kształcie trójkąta równobocznego odcięto naroża, tak jak pokazano na rysunku i otrzymano sześciokąt foremny o bokach długości 3.
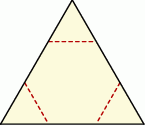
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Kartonik był trójkątem o obwodzie 27. | P | F |
| Suma pól odciętych naroży jest dwa razy mniejsza od pola sześciokąta. | P | F |
Pola dwóch trójkątów równobocznych są równe odpowiednio 7 i 63.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód drugiego trójkąta jest 9 razy większy od obwodu pierwszego trójkąta. | P | F |
Pierwszy trójkąt jest podobny do drugiego w skali  | P | F |
W układzie współrzędnych zaznaczono wierzchołki 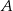 i
i 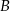 rombu
rombu 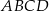 oraz jedną z jego osi symetrii.
oraz jedną z jego osi symetrii.
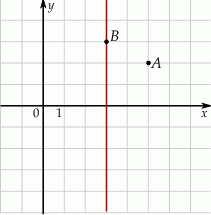
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Pole rombu 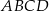 jest równe
jest równe
A) 2 B) 4 C) 6 D) 8
Dwie proste równoległe 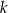 i
i 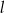 przecięto prostymi
przecięto prostymi 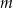 i
i  w sposób przedstawiony na rysunku.
w sposób przedstawiony na rysunku.
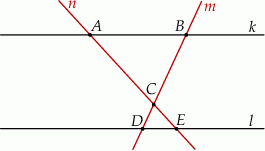
Czy trójkąty 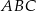 i
i 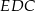 są przystające? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D.
są przystające? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D.
| Tak | Nie |
| ponieważ | |
| A) | te trójkąty mają wspólny wierzchołek. |
| B) | te trójkąty mają boki różnej długości. |
| C) | te trójkąty mają odpowiednie kąty równej miary. |
| D) | te trójkąty mają boki równoległe. |
W tabeli przedstawiono liczbę i rodzaj kul umieszczonych w czterech pudełkach. Z każdego pudełka losujemy jedną kulę.
| Liczba kul zielonych | Liczba kul niebieskich | Liczba kul czerwonych | |
| Pudełko nr 1 | 4 | 8 | 5 |
| Pudełko nr 2 | 7 | 16 | 9 |
| Pudełko nr 3 | 2 | 7 | 3 |
| Pudełko nr 4 | 7 | 12 | 5 |
Dokończ zdanie, wybierając odpowiedź spośród podanych.
Prawdopodobieństwo wylosowania niebieskiej kuli jest największe, gdy kulę losujemy z pudełka nr
A) 1 B) 2 C) 3 D) 4
Kształt i wymiary drewnianej zabawki przedstawiono na rysunku.
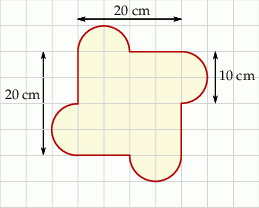
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Powierzchnia tej zabawki (w 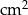 ) jest równa
) jest równa
A) 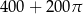 B)
B) 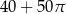 C)
C) 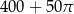 D)
D) 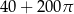
Nadajnik telekomunikacyjny znajduje się w punkcie 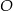 (niezaznaczonym na rysunku), który jest jednakowo oddalony od trzech dróg łączących miasta
(niezaznaczonym na rysunku), który jest jednakowo oddalony od trzech dróg łączących miasta 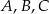 .
.
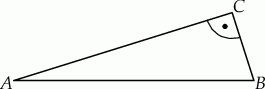
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Punkt 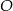 jest punktem przecięcia dwusiecznych kątów trójkąta jest punktem przecięcia dwusiecznych kątów trójkąta 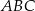 . . | P | F |
Punkt 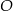 jest środkiem okręgu opisanego na trójkącie jest środkiem okręgu opisanego na trójkącie 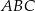 . . | P | F |
Do okręgu o środku 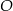 należą punkty
należą punkty 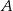 i
i 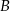 . Okrąg ma promień 48, a łuk
. Okrąg ma promień 48, a łuk 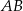 ma długość
ma długość 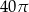 .
.
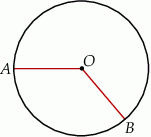
Jaką miarę ma kąt środkowy oparty na tym łuku?
Wybierz odpowiedź spośród podanych.
A) 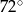 B)
B) 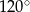 C)
C) 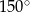 D)
D) 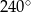
Dany jest trapez prostokątny 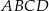 , w którym trójkąt
, w którym trójkąt 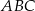 jest trójkątem równobocznym o boku długości 6 cm.
jest trójkątem równobocznym o boku długości 6 cm.
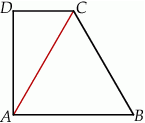
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
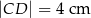 | P | F |
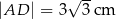 | P | F |
Na rysunku przedstawiono walec, stożek i kulę oraz niektóre ich wymiary.
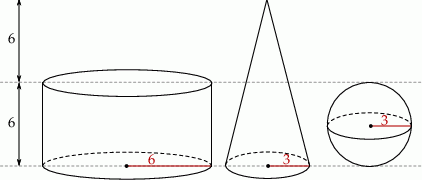
Na podstawie informacji przedstawionych na rysunku wybierz zdanie fałszywe.
A) Objętość kuli jest równa objętości stożka.
B) Objętość walca jest 3 razy większa od objętości stożka.
C) Objętość walca jest 6 razy większa od objętości kuli.
D) Suma objętości stożka i kuli jest mniejsza od objętości walca.
Uzasadnij, że jeśli liczba jest podzielna przez 18 i przez 84, to jest podzielna przez 252.
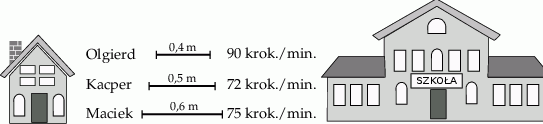
Trzech braci: Olgierd, Kacper i Maciek pokonują tę samą drogę z domu do szkoły. Olgierd stawia kroki długości 0,4 m w tempie 90 kroków na minutę, Kacper stawia kroki długości 0,5 m w tempie 72 kroków na minutę, a Maciek stawia kroki długości 0,6 m w tempie 75 kroków na minutę. Olgierd i Kacper przyszli do szkoły dokładnie w tym samym momencie, przy czym Kacper zrobił 900 kroków mniej od Olgierda. Oblicz, ile minut zajmie droga do szkoły Maćkowi.
Na rysunku przedstawiono bryłę, której każda ściana jest albo kwadratem, albo trójkątem równobocznym. Kwadratami są też czworokąty 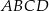 i
i 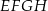 . Każda krawędź ma długość 4. Jaką objętość ma ta bryła? Zapisz obliczenia.
. Każda krawędź ma długość 4. Jaką objętość ma ta bryła? Zapisz obliczenia.