Zadanie nr 6485778
Pewna maszyna wykonuje śruby o średnicy 14 mm. Dokonano kontroli jakości wykonywanych śrub i jej wyniki zebrano w tabeli.
| Średnica w mm | 13,8 | 13,9 | 14 | 14,1 | 14,2 |
| Liczba śrub | 8 | 17 | 48 | 13 | 14 |
Opierając się na podanych danych.
- Oblicz średnią średnicę śruby.
- Oblicz prawdopodobieństwo wyprodukowania śruby o średnicy z przedziału
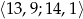 .
. - Oblicz odchylenie standardowe średnicy śruby. Wynik podaj z dokładnością do 0,01.
Rozwiązanie
- W sumie dokonano pomiaru
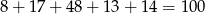
śrub, więc średnia arytmetyczna jest równa
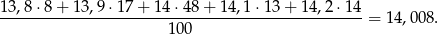
Odpowiedź: 14,008 mm - Liczymy
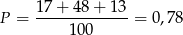
Odpowiedź: 0,78 - Liczymy wariancję podanych danych.
![1 ---[(13,8 − 14,0 08)2 ⋅8 + (13 ,9− 1 4,008)2 ⋅17+ (14− 14,008 )2 ⋅48+ 100 + (14,1 − 14,00 8)2 ⋅13 + (14 ,2 − 1 4,008)2 ⋅ 14] = 1 = ---[0,208 2 ⋅8 + 0,108 2 ⋅17 + 0,00 82 ⋅48 + 0 ,0 922 ⋅1 3+ 0,1922 ⋅ 14] = 100 = 1-,1736 = 0,011736. 100](https://img.zadania.info/zad/6485778/HzadR3x.gif)
Zatem odchylenie standardowe jest równe
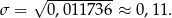
Odpowiedź: 0,11 mm

