/Szkoła średnia/Zadania maturalne/Matura 2010
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 27 marca 2010 Czas pracy: 180 minut
Wewnątrz prostokąta 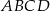 o wymiarach
o wymiarach 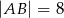 i
i 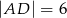 wybrano dwa punkty
wybrano dwa punkty 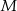 i
i 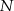 takie, że
takie, że 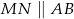 oraz
oraz 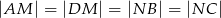 . Przy jakiej odległości punktów
. Przy jakiej odległości punktów 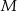 i
i 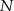 suma kwadratów długości odcinków
suma kwadratów długości odcinków 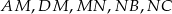 jest najmniejsza?
jest najmniejsza?
Rozwiązaniem nierówności 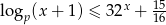 z niewiadomą
z niewiadomą  jest zbiór
jest zbiór 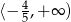 . Wyznacz
. Wyznacz 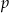 .
.
Różnica między pierwszym a siódmym wyrazem ciągu geometrycznego jest równa 63, a różnica między wyrazem pierwszym a czwartym jest równa 72. Oblicz sumę pierwszych 7 wyrazów tego ciągu.
W urnie znajduje się 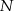 losów, przy czym
losów, przy czym 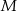 z nich to losy wygrywające (
z nich to losy wygrywające (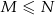 ). Wybieramy losowo
). Wybieramy losowo  losów z urny (
losów z urny (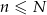 ) i niech
) i niech 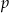 oznacza prawdopodobieństwo, że dokładnie
oznacza prawdopodobieństwo, że dokładnie 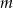 spośród tych losów to losy wygrywające (
spośród tych losów to losy wygrywające (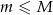 oraz
oraz 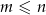 ). Uzasadnij, że
). Uzasadnij, że
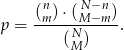
Na wysokości  trójkąta
trójkąta  wybrano punkt
wybrano punkt 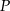 taki, że
taki, że 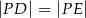 , gdzie
, gdzie 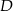 i
i 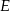 są rzutami tego punktu odpowiednio na boki
są rzutami tego punktu odpowiednio na boki 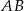 i
i 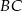 . Wiedząc, że
. Wiedząc, że 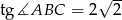 oblicz iloraz
oblicz iloraz  .
.
Wyznacz równanie okręgu, który jest obrazem okręgu 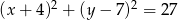 w jednokładności o środku
w jednokładności o środku 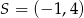 i skali
i skali 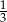 .
.
Wykaż, że jeżeli liczby całkowite 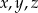 spełniają równanie
spełniają równanie 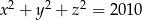 to co najwyżej jedna z liczb
to co najwyżej jedna z liczb 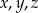 dzieli się przez 4.
dzieli się przez 4.
Sprzedawca zegarków kupił w hurtowni za 5746 złotych dwa rodzaje zegarków: damskie i męskie, przy czym kupił trzy razy więcej zegarków damskich niż męskich. Przy ponownym zakupie takiej samej ilości zegarków, otrzymał 10% rabatu na cenę zakupu zegarka damskiego oraz 10 zł upustu na cenę zakupu zegarka męskiego. Dzięki otrzymanym rabatom, łączny koszt zakupu zmalał do 5265 zł. Wiedząc, że po udzieleniu rabatu, cena męskiego zegarka była dwa razy wyższa od ceny zegarka damskiego, oblicz pierwotne ceny zegarków.
W graniastosłupie prawidłowym sześciokątnym poprowadzono płaszczyznę, która przechodzi przez dłuższą przekątną dolnej podstawy oraz przez jedną z krawędzi górnej podstawy. Płaszczyzna ta wyznacza przekrój graniastosłupa, który jest trapezem równoramiennym. Wiedząc, że w trapez ten można wpisać okrąg o promieniu 1, oblicz objętość graniastosłupa.
Rozwiąż równanie 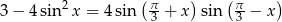 .
.
Wyznacz wszystkie wartości parametru 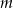 , dla których równanie
, dla których równanie
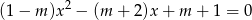
ma przynajmniej jedno rozwiązanie ujemne.

