/Szkoła średnia/Zadania maturalne/Matura 2010
Egzamin Maturalny
z Matematyki poziom podstawowy 5 maja 2010 Czas pracy: 170 minut
Zadania zamknięte
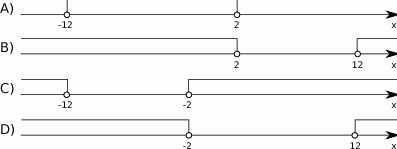
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 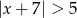 .
.
Spodnie po obniżce ceny o 30% kosztują 126 zł. Ile kosztowały spodnie przed obniżką?
A) 163,80 zł B) 180 zł C) 294 zł D) 420 zł
Liczba 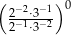 jest równa
jest równa
A) 1 B) 4 C) 9 D) 36
Liczba 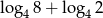 jest równa
jest równa
A) 1 B) 2 C) 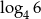 D)
D) 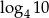
Dane są wielomiany 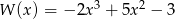 oraz
oraz 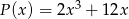 . Wielomian
. Wielomian 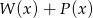 jest równy
jest równy
A) 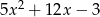
B) 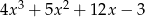
C) 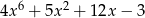
D) 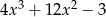
Rozwiązaniem równania 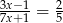 jest
jest
A) 1 B)  C)
C) 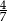 D) 7
D) 7
Do zbioru rozwiązań nierówności 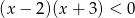 należy liczba
należy liczba
A) 9 B) 7 C) 4 D) 1
Wykresem funkcji kwadratowej 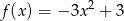 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie
A) 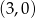 B)
B) 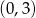 C)
C) 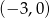 D)
D) 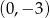
Prosta o równaniu 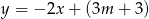 przecina w układzie współrzędnych oś
przecina w układzie współrzędnych oś 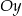 w punkcie
w punkcie 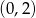 . Wtedy
. Wtedy
A) 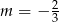 B)
B) 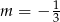 C)
C) 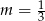 D)
D) 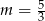
Na rysunku jest przedstawiony wykres funkcji 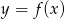 .
.
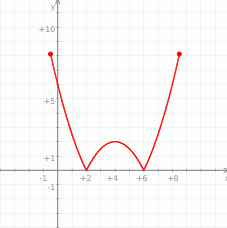
Które równanie ma dokładnie trzy rozwiązania?
A) 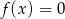 B)
B) 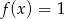 C)
C) 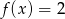 D)
D) 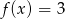
W ciągu arytmetycznym 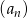 dane są:
dane są: 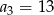 i
i 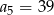 . Wtedy wyraz
. Wtedy wyraz 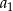 jest równy
jest równy
A) 13 B) 0 C) -13 D) -26
W ciągu geometrycznym 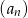 dane są:
dane są: 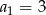 i
i 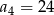 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 8 B) 2 C) 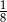 D)
D) 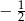
Liczba przekątnych siedmiokąta foremnego jest równa
A) 7 B) 14 C) 21 D) 28
Kąt  jest ostry i
jest ostry i 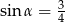 . Wartość wyrażenia
. Wartość wyrażenia 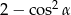 jest równa
jest równa
A) 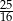 B)
B)  C)
C) 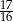 D)
D) 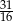
Okrąg opisany na kwadracie ma promień 4. Długość boku tego kwadratu jest równa
A) 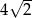 B)
B) 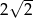 C) 8 D) 4
C) 8 D) 4
Podstawa trójkąta równoramiennego ma długość 6, a ramię ma długość 5. Wysokość opuszczona na podstawę ma długość
A) 3 B) 4 C) 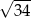 D)
D) 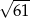
Odcinki 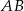 i
i 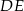 są równoległe. Długości odcinków
są równoległe. Długości odcinków 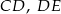 i
i 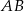 są odpowiednio równe 1, 3 i 9.
są odpowiednio równe 1, 3 i 9.
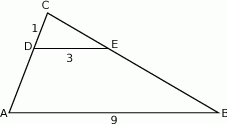
Długość odcinka 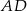 jest równa
jest równa
A) 2 B) 3 C) 5 D) 6
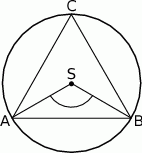
Punkty 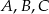 leżące na okręgu o środku
leżące na okręgu o środku 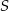 są wierzchołkami trójkąta równobocznego. Miara zaznaczonego na rysunku kąta środkowego
są wierzchołkami trójkąta równobocznego. Miara zaznaczonego na rysunku kąta środkowego 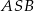 jest równa
jest równa
A) 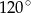 B)
B) 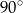 C)
C) 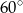 D)
D) 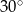
Latawiec ma wymiary podane na rysunku. Powierzchnia zacieniowanego trójkąta jest równa
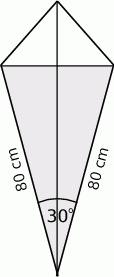
A) 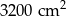 B)
B) 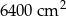 C)
C) 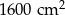 D)
D) 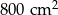
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 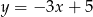 jest równy
jest równy
A) 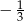 B) -3 C)
B) -3 C) 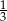 D) 3
D) 3
Wskaż równanie okręgu o promieniu 6.
A) 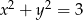 B)
B) 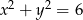 C)
C) 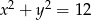 D)
D) 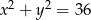
Punkty 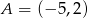 i
i 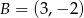 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 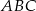 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 30 B) 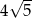 C)
C) 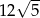 D) 36
D) 36
Pole powierzchni całkowitej prostopadłościanu o wymiarach 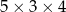 jest równe
jest równe
A) 94 B) 60 C) 47 D) 20
Ostrosłup ma 18 wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa
A) 11 B) 18 C) 27 D) 34
Średnia arytmetyczna dziesięciu liczb 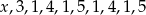 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 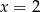 B)
B) 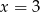 C)
C) 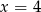 D)
D) 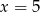
Zadania otwarte
Rozwiąż nierówność 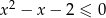 .
.
Rozwiąż równanie 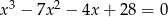 .
.
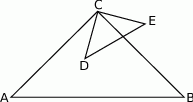
Trójkąty prostokątne równoramienne 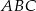 i
i 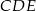 są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku
są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku 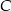 jest prosty). Wykaż, że
jest prosty). Wykaż, że 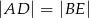 .
.
Kąt  jest ostry i
jest ostry i 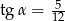 . Oblicz
. Oblicz 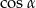 .
.
Wykaż, że jeśli 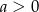 , to
, to 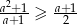 .
.
W trapezie prostokątnym krótsza przekątna dzieli go na trójkąt prostokątny i trójkąt równoboczny. Dłuższa podstawa trapezu jest równa 6. Oblicz obwód tego trapezu.
Podstawą ostrosłupa 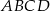 jest trójkąt
jest trójkąt 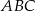 . Krawędź
. Krawędź 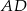 jest wysokością ostrosłupa (zobacz rysunek).
jest wysokością ostrosłupa (zobacz rysunek).
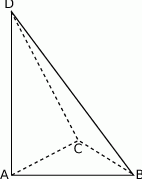
Oblicz objętość ostrosłupa 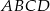 , jeśli wiadomo, że
, jeśli wiadomo, że 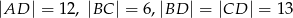 .
.
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 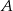 polegającego na tym, że w pierwszym rzucie otrzymamy parzystą liczbę oczek i iloczyn liczb oczek w obu rzutach będzie podzielny przez 12. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
polegającego na tym, że w pierwszym rzucie otrzymamy parzystą liczbę oczek i iloczyn liczb oczek w obu rzutach będzie podzielny przez 12. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
W dwóch hotelach wybudowano prostokątne baseny. Basen w pierwszym hotelu ma powierzchnię 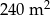 . Basen w drugim hotelu ma powierzchnię
. Basen w drugim hotelu ma powierzchnię 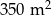 oraz jest o 5 m dłuższy i 2 m szerszy niż w pierwszym hotelu. Oblicz, jakie wymiary mogą mieć baseny w obu hotelach. Podaj wszystkie możliwe odpowiedzi.
oraz jest o 5 m dłuższy i 2 m szerszy niż w pierwszym hotelu. Oblicz, jakie wymiary mogą mieć baseny w obu hotelach. Podaj wszystkie możliwe odpowiedzi.

