/Szkoła średnia/Zadania maturalne/Matura 2010
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 24 kwietnia 2010 Czas pracy: 170 minut
Zadania zamknięte
Liczba 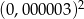 jest równa
jest równa
A) 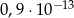 B)
B) 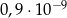 C)
C) 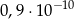 D)
D) 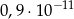
Oprocentowanie kredytu zwiększono z 10% do 15%. Zatem oprocentowanie kredytu wzrosło o
A) 50% B) 15% C) 5% D) 75%
Jeżeli 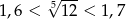 to liczba
to liczba 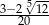 należy do przedziału
należy do przedziału
A) 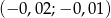 B)
B) 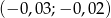 C)
C) 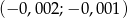 D)
D) 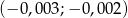
Dane są zbiory 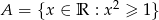 i
i 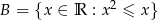 . Zatem zbiór
. Zatem zbiór 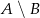 jest równy
jest równy
A) 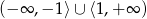
B) 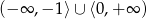
C) 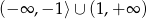
D) 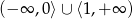
Liczba 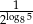 jest równa
jest równa
A) 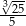 B)
B) 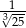 C)
C) 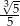 D)
D) 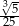
Przedział 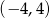 jest rozwiązaniem nierówności
jest rozwiązaniem nierówności
A) 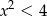 B)
B) 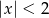 C)
C) 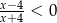 D)
D) 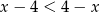
Odcinek 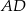 jest dwusieczną w trójkącie równoramiennym
jest dwusieczną w trójkącie równoramiennym 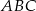 poprowadzoną do ramienia
poprowadzoną do ramienia 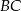 .
.
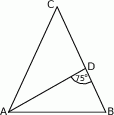
Jeżeli 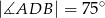 to miara kąta przy wierzchołku
to miara kąta przy wierzchołku 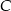 jest równa
jest równa
A) 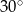 B)
B) 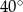 C)
C) 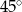 D)
D) 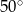
Wskaż wzór funkcji, której wykres można otrzymać przez przesunięcie wykresu funkcji 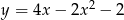 .
.
A) 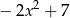 B)
B) 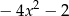 C)
C) 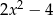 D)
D) 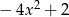
Która z podanych prostych jest styczna do okręgu 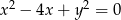 ?
?
A) 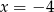 B)
B) 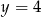 C)
C) 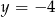 D)
D) 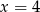
Rozwiązaniem równania 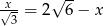 jest liczba
jest liczba
A) 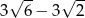 B)
B) 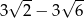 C)
C) 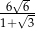 D)
D) 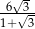
Liczby 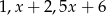 są kolejnymi wyrazami ciągu geometrycznego. Zatem liczba
są kolejnymi wyrazami ciągu geometrycznego. Zatem liczba  spełnia warunek
spełnia warunek
A) 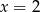 B)
B) 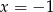 C)
C) 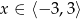 D)
D) 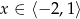
Przybliżona długość przeciwprostokątnej trójkąta prostokątnego przedstawionego na rysunku jest równa

A) 5,49 B) 5,9 C) 5,85 D) 5,5
Który z czworokątów ma zawsze więcej niż dwie osie symetrii?
A) deltoid B) prostokąt C) kwadrat D) romb
Funkcja 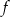 określona jest wzorem
określona jest wzorem
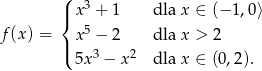
Ile miejsc zerowych ma ta funkcja?
A) 0 B) 1 C) 2 D) 3
Ciąg 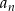 dany jest wzorem
dany jest wzorem 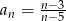 , gdzie
, gdzie 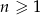 oraz
oraz 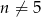 . Liczba wyrazów całkowitych tego ciągu to
. Liczba wyrazów całkowitych tego ciągu to
A) 1 B) 2 C) 3 D) 4
Przekątna 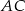 jest średnicą okręgu opisanego na czworokącie
jest średnicą okręgu opisanego na czworokącie 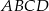 . Punkt przecięcia przekątnych dzieli przekątną
. Punkt przecięcia przekątnych dzieli przekątną 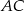 na odcinki o długościach 3 i 6. Zatem długość okręgu opisanego na czworokącie
na odcinki o długościach 3 i 6. Zatem długość okręgu opisanego na czworokącie 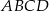 jest równa
jest równa
A) 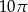 B)
B) 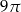 C)
C) 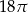 D)
D) 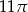
Wielomiany 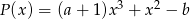 i
i 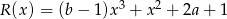 są równe. Zatem liczba
są równe. Zatem liczba 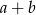
A) należy do zbioru 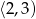
B) jest większa od 3
C) należy do zbioru 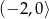
D) jest mniejsza od -2
Która z podanych prostych nie ma punktów wspólnych z trzecią ćwiartką układu współrzędnych?
A) 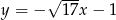 B)
B) 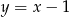 C)
C) 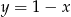 D)
D) 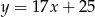
Różnica długości podstaw trapezu równoramiennego o kącie ostrym 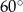 i ramieniu długości 12 może być równa
i ramieniu długości 12 może być równa
A) 6 B) 8 C) 9 D) 12
Na rysunku przedstawiono wykres funkcji 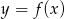 .
.
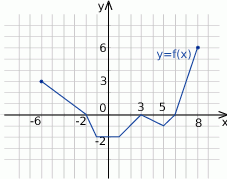
Zbiorem wartości funkcji 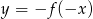 jest
jest
A) 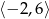 B)
B) 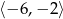 C)
C) 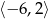 D)
D) 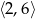
Mediana danych zawartych w tabeli liczebności jest równa 3.
| Wartość | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczebność | 3 | 4 |  | 1 | 2 | 6 |
Zatem  może być równe
może być równe
A) 0 B) 1 C) 2 D) 3
Wykonując rozmowę telefoniczną płacimy 63 grosze za rozpoczęcie połączenia oraz 42 grosze za każdą minutę połączenia. Ile minut trwała rozmowa, której łączny koszt wyniósł 16,17 zł?
A) 38 B) 36 C) 43 D) 37
Z pudełka zawierającego dwa rodzaje monet wybieramy losowo dwie. Prawdopodobieństwo wybrania co najmniej jednej monety dwuzłotowej jest równe 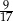 , a prawdopodobieństwo wybrania co najmniej jednej monety pięciozłotowej jest równe
, a prawdopodobieństwo wybrania co najmniej jednej monety pięciozłotowej jest równe 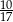 . Zatem prawdopodobieństwo wybrania dokładnie jednej monety dwuzłotowej jest równe
. Zatem prawdopodobieństwo wybrania dokładnie jednej monety dwuzłotowej jest równe
A) 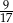 B)
B) 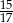 C)
C) 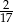 D)
D) 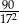
Prostopadłościan dzielimy na części prowadząc dwie płaszczyzny równoległe do jego podstaw, które dzielą krawędź boczną w stosunku 5:1:2. Jaki procent objętości całego prostopadłościanu stanowi objętość najmniejszej z utworzonych części?
A) 15% B) 25% C) 17% D) 12,5%
Wyrazami ciągu 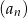 danego wzorem
danego wzorem 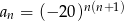
A) są zawsze liczby mniejsze od 1
B) są zawsze liczby dodatnie
C) są zawsze liczby ujemne
D) są zarówno liczby dodatnie, jak i ujemne
Zadania otwarte
Wyznacz najmniejszą wartość funkcji 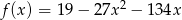 na przedziale
na przedziale 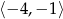 .
.
Udowodnij, że jeżeli środek okręgu opisanego na trójkącie leży na jednym z jego boków, to trójkąt ten jest prostokątny.
Oblicz wartość wyrażenia 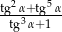 jeżeli
jeżeli 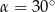 .
.
Na prostej 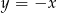 wyznacz punkt, który jest równo odległy od początku układu współrzędnych oraz od punktu
wyznacz punkt, który jest równo odległy od początku układu współrzędnych oraz od punktu 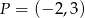 .
.
Trapez, w którym jedna z podstaw jest dwa razy dłuższa od drugiej, podzielono odcinkiem łączącym środki ramion trapezu na dwa czworokąty. Oblicz stosunek pól otrzymanych czworokątów.
Zbiór rozwiązań równania 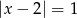 jest podzbiorem zbioru rozwiązań równania
jest podzbiorem zbioru rozwiązań równania 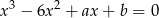 . Wyznacz
. Wyznacz  i
i 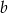 .
.
Zosia przez 30 dni kwietnia wrzucała do skarbonki pieniądze, przy czym każdego kolejnego dnia wrzucała o 2 zł więcej niż w dniu poprzednim. Wiedząc, że średnio wrzucała 33 zł złotych dziennie, oblicz ile pieniędzy wrzuciła do skarbonki 8 kwietnia.
Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: 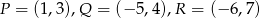 .
.

