/Szkoła średnia/Zadania maturalne/Matura 2010
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 13 marca 2010 Czas pracy: 170 minut
Zadania zamknięte
Liczba 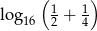 jest równa
jest równa
A)  B) 6 C)
B) 6 C) 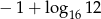 D) -6
D) -6
Cena długopisu po 3 podwyżkach o 50% i dwóch obniżkach o 20% wzrosła o 2,32 zł. Nowa cena długopisu jest równa
A) 3,42 zł B) 2 zł C) 4,32 zł D) 2,34 zł
Wykres funkcji kwadratowej 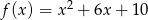 powstaje z wykresu funkcji
powstaje z wykresu funkcji 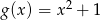 przez przesunięcie o 3 jednostki
przez przesunięcie o 3 jednostki
A) w prawo B) w lewo C) w górę D) w dół
Liczbą odwrotną do 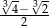 jest
jest
A) 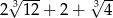 B)
B) 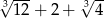 C)
C) 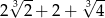 D)
D) 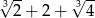
Liczba 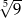 jest większa od
jest większa od
A) 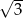 B)
B) 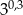 C)
C) 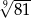 D) 3
D) 3
Para liczb 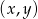 , która spełnia równanie
, która spełnia równanie 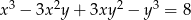 to
to
A) 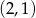 B)
B) 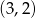 C)
C) 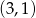 D)
D) 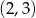
Na tablicy wypisano kolejne wyrazy pewnego ciągu arytmetycznego
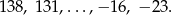
Ile liczb napisano na tablicy?
A) 21 B) 22 C) 23 D) 24
Równanie 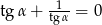 , gdzie
, gdzie  jest kątem ostrym
jest kątem ostrym
A) ma dokładnie jedno rozwiązanie
B) ma dokładnie dwa rozwiązania
C) ma nieskończenie wiele rozwiązań
D) nie ma rozwiązań
Do zbioru rozwiązań nierówności 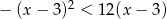 należy liczba
należy liczba
A) 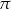 B)
B) 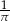 C)
C) 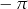 D)
D) 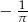
Ciąg 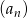 dany jest wzorem,
dany jest wzorem, 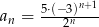 . Ciąg
. Ciąg 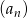 jest ciągiem
jest ciągiem
A) rosnącym B) malejącym C) arytmetycznym D) geometrycznym
Punkt 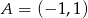 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 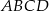 , którego bok
, którego bok 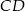 zawiera się w prostej
zawiera się w prostej 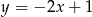 . Podstawa
. Podstawa 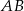 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 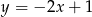 B)
B) 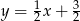 C)
C) 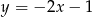 D)
D) 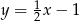
Punkt 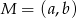 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 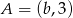 i
i 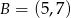 . Wówczas
. Wówczas
A) 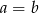 B)
B) 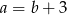 C)
C) 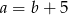 D)
D) 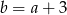
Jeżeli 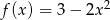 to funkcja
to funkcja 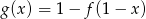 ma wzór
ma wzór
A) 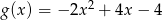
B) 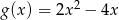
C) 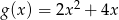
D) 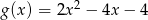
Do okręgu o środku 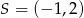 i promieniu
i promieniu 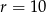 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 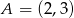 B)
B) 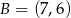 C)
C) 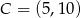 D)
D) 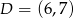
Przez wierzchołek 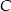 trójkąta prostokątnego
trójkąta prostokątnego 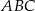 poprowadzono styczną do okręgu opisanego na tym trójkącie.
poprowadzono styczną do okręgu opisanego na tym trójkącie.
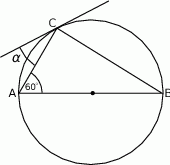
Jeżeli 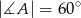 to miara kąta
to miara kąta  jest równa
jest równa
A) 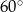 B)
B) 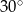 C)
C) 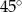 D)
D) 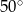
Wyraz wolny wielomianu 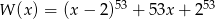 jest równy
jest równy
A) 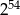 B) 0 C)
B) 0 C) 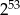 D) 53
D) 53
Ile można utworzyć liczb czterocyfrowych podzielnych przez 20, o cyfrach należących do zbioru 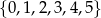 ?
?
A) 12 B) 60 C) 90 D) 20
Które z równań należy wpisać w miejsce gwiazdek, aby układ równań 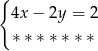 miał nieskończenie wiele rozwiązań?
miał nieskończenie wiele rozwiązań?
A) 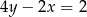 B)
B) 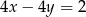 C)
C) 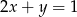 D)
D) 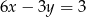
Promień okręgu wpisanego w trójkąt równoboczny jest o 2 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 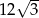 B)
B) 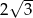 C)
C) 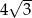 D)
D) 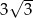
Zdarzenia losowe 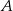 i
i 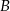 są rozłączne oraz
są rozłączne oraz 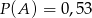 . Zatem prawdopodobieństwo zdarzenia
. Zatem prawdopodobieństwo zdarzenia 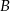 może być równe
może być równe
A) 0,63 B) 0,53 C) 0,43 D) 1
Pole podstawy stożka jest trzy razy mniejsze od jego pola powierzchni bocznej. Wówczas kąt  rozwarcia stożka spełnia warunek
rozwarcia stożka spełnia warunek
A) 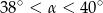 B)
B) 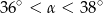 C)
C) 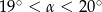 D)
D) 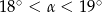
Które z podanych równań nie ma rozwiązań
A) 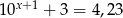 B)
B) 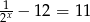 C)
C) 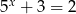 D)
D) 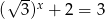
Zadania otwarte
Oblicz wysokość trapezu o podstawach długości 18 i 14 oraz ramionach długości 3.
Rozwiąż równanie 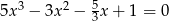 .
.
Wiedząc, że 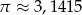 oblicz
oblicz 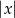 , gdzie
, gdzie 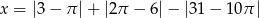 .
.
Wykaż, że środki boków rombu są wierzchołkami prostokąta.
Wiadomo, że funkcja liniowa 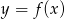 przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy
przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy 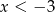 . Ponadto,
. Ponadto, 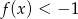 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 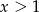 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 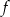 .
.
W pewnej szkole 20% uczniów uczęszcza na kółko plastyczne, a 34% uczniów uczęszcza na kółko muzyczne. Wiadomo ponadto, że 58% uczniów nie uczęszcza na żadne z tych kółek. Oblicz jakie jest prawdopodobieństwo, że losowy wybrany uczeń tej szkoły uczęszcza jednocześnie na kółko plastyczne i muzyczne.
Wyznacz wyraz ogólny ciągu geometrycznego 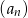 , w którym
, w którym 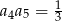 oraz
oraz 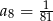 .
.
W prostokącie 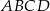 , w którym
, w którym 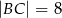 połączono wierzchołek
połączono wierzchołek 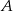 z punktem
z punktem 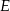 leżącym na boku
leżącym na boku 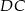 . Odcinek ten przeciął przekątną
. Odcinek ten przeciął przekątną 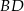 w punkcie
w punkcie 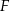 .
.
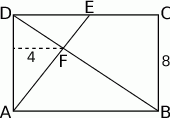
Wiedząc, że odległość punktu 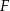 od boku
od boku 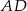 jest równa 4, oraz że
jest równa 4, oraz że 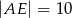 oblicz długość boku
oblicz długość boku 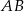 prostokąta.
prostokąta.
Jeżeli skrócimy wysokość trapezu o polu 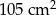 o 2 cm i jednocześnie wydłużymy każdą z jego podstaw o 6 cm, to pole trapezu nie ulegnie zmianie. Wyznacz długość wysokości trapezu (przed zmianą).
o 2 cm i jednocześnie wydłużymy każdą z jego podstaw o 6 cm, to pole trapezu nie ulegnie zmianie. Wyznacz długość wysokości trapezu (przed zmianą).

