/Szkoła średnia/Zadania maturalne/Matura 2010
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 10 kwietnia 2010 Czas pracy: 170 minut
Zadania zamknięte
Liczba 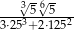 jest równa
jest równa
A) 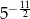 B)
B) 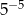 C)
C) 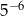 D)
D) 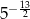
Jeżeli 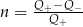 i
i 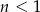 to
to
A) 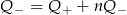 B)
B) 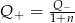 C)
C) 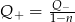 D)
D) 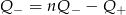
Na rysunku 1 jest przedstawiony wykres funkcji 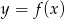 .
.
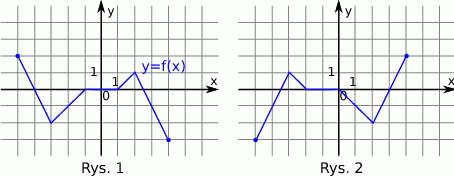
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 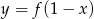 B)
B) 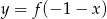 C)
C) 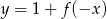 D)
D) 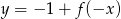
Najmniejszą liczbą całkowitą należącą do dziedziny funkcji 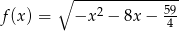 jest
jest
A) -2 B) -3 C) -4 D) -5
Do wykresu funkcji wykładniczej 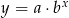 należą punkty
należą punkty 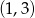 i
i 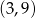 . Zatem liczba
. Zatem liczba 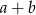 jest równa
jest równa
A) 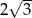 B) 12 C)
B) 12 C) 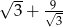 D)
D) 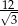
Liczba 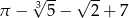 jest rozwiązaniem równania
jest rozwiązaniem równania 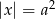 z niewiadomą
z niewiadomą  . Która z podanych liczb jest również rozwiązaniem tego równania?
. Która z podanych liczb jest również rozwiązaniem tego równania?
A) 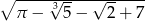
B) 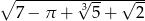
C) 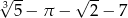
D) 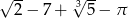
Połączono środki boków trójkąta 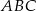 otrzymując trójkąt
otrzymując trójkąt 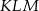 . O ile procent pole trójkąta
. O ile procent pole trójkąta 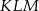 jest mniejsze od pola trójkąta
jest mniejsze od pola trójkąta 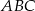 ?
?
A) 80% B) 75% C) 50% D) 25%
Na podstawie fragmentu wykresu funkcji kwadratowej 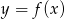 wskaż, które zdanie jest prawdziwe.
wskaż, które zdanie jest prawdziwe.
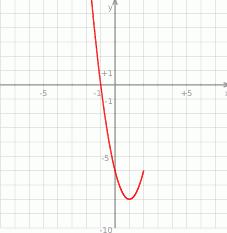
A) Jeżeli 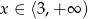 to
to 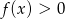 .
.
B) Do wykresu funkcji należy punkt 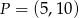 .
.
C) Miejscami zerowymi funkcji 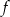 są liczby: -1 oraz 4.
są liczby: -1 oraz 4.
D) Wartości funkcji są dodatnie dla 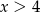 .
.
Dwa wyrazy ciągu arytmetycznego o wyrazach całkowitych są równe 200 i 101. Różnica tego ciągu może być równa
A) 5 B) 18 C) 11 D) 199
Wartość wyrażenia 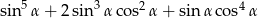 jest równa
jest równa
A) 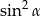 B)
B) 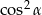 C)
C) 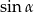 D)
D) 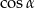
Punkty 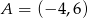 i
i 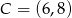 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 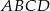 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 4 B) 52 C) 104 D) 26
Ciąg 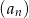 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 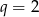 , w którym
, w którym 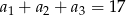 . Suma
. Suma 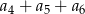 jest równa
jest równa
A) 136 B) 68 C) 34 D) 289
Wykres funkcji 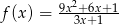 i prosta
i prosta 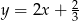
A) pokrywają się
B) mają jeden punkt wspólny
C) są rozłączne
D) mają dwa punkty wspólne
Kąt wpisany w okrąg o promieniu 6, który jest oparty na łuku długości 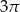 ma miarę
ma miarę
A) 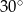 B)
B) 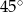 C)
C) 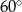 D)
D) 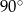
Jeżeli 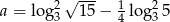 to liczba
to liczba  jest równa
jest równa
A) 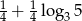 B)
B) 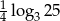 C)
C) 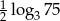 D)
D) 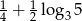
Przekątna prostopadłościanu o wymiarach 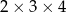 ma długość
ma długość
A) 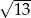 B)
B) 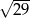 C) 5 D) 6
C) 5 D) 6
Ze zbioru 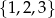 wybieramy dwie liczby (mogą się powtarzać), a ze zbioru
wybieramy dwie liczby (mogą się powtarzać), a ze zbioru 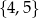 jedną liczbę. Na ile sposobów można to zrobić tak, aby otrzymane 3 liczby były długościami boków pewnego trójkąta?
jedną liczbę. Na ile sposobów można to zrobić tak, aby otrzymane 3 liczby były długościami boków pewnego trójkąta?
A) 2 B) 3 C) 4 D) 6
Wielomian 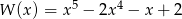
A) jest iloczynem wielomianów 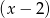 i
i 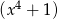
B) ma trzy miejsca zerowe
C) ma dwa miejsca zerowe
D) jest różnicą wielomianów 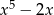 i
i 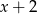
Jacek planując wycieczkę zagraniczną postanowił ocenić kilka ofert przyznając punkty w trzech kategoriach
| Nr oferty | Cena | Atrakcyjność | Dostępność |
| I | 1 | 3 | 4 |
| II | 2 | 2 | 2 |
| III | 3 | 1 | 2 |
Aby porównać ze sobą oferty postanowił policzyć średnią ważoną przyznanych punktów stosując następujące wagi:
| Kategoria | Cena | Atrakcyjność | Dostępność |
| Waga | 50 | 35 | 15 |
Wycieczki, dla których policzona średnia jest najwyższa to
A) I i II B) II i III C) I i III D) III
Przekątne podzieliły równoległobok na cztery trójkąty o polach 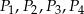 .
.
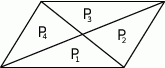
Który z podanych warunków może nie być spełniony?
A) 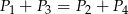 B)
B) 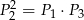 C)
C) 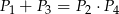 D)
D) 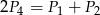
Zadania otwarte
Motocyklista drogę z miasta 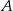 do miasta
do miasta 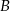 pokonał ze średnią prędkością 84 km/h. Pokonanie drogi powrotnej zajęło mu o godzinę dłużej, a średnia prędkość wyniosła 56 km/h. Oblicz odległość między miastami
pokonał ze średnią prędkością 84 km/h. Pokonanie drogi powrotnej zajęło mu o godzinę dłużej, a średnia prędkość wyniosła 56 km/h. Oblicz odległość między miastami 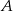 i
i 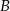 .
.
Wyznacz największą wartość funkcji 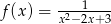 .
.
Dziesięć kul bilardowych średnicy 6 cm umieszczono w prostokątnym pudełku tak jako pokazano to na rysunku.
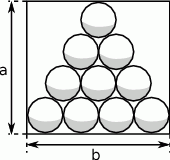
Wyznacz wymiary  i
i 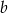 tego pudełka.
tego pudełka.
Przekątne podzieliły czworokąt na 4 trójkąty.
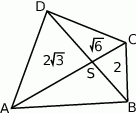
Korzystając z podanych pól trzech z tych trójkątów, wyznacz pole trójkąta 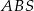 .
.
W urnie znajduje się 27 kul w dwóch kolorach. Wiadomo, że wśród każdych 13 kul wybranych z urny jest co najmniej jedna czarna, a wśród każdych 16 kul jest co najmniej jedna biała. Ile białych kul znajduje się w urnie?
W jakim stosunku należy zmieszać 14 i 6 procentowe roztwory chlorku sodu, aby otrzymać roztwór 8 procentowy?
Wyznacz równanie okręgu symetrycznego do okręgu 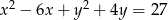 względem prostej
względem prostej 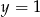 .
.
Trójkąt prostokątny ma boki długości 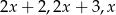 . Wyznacz
. Wyznacz  oraz promień okręgu wpisanego w ten trójkąt.
oraz promień okręgu wpisanego w ten trójkąt.
Dane są punkty 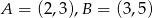 i
i 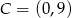 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 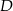 , dla którego czworokąt
, dla którego czworokąt 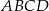 jest trapezem prostokątnym, którego kąt przy wierzchołku
jest trapezem prostokątnym, którego kąt przy wierzchołku 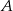 jest prosty.
jest prosty.
Pole powierzchni całkowitej 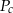 stożka oraz jego pole podstawy
stożka oraz jego pole podstawy 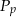 spełniają równanie
spełniają równanie 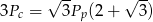 . Oblicz miarę kąta rozwarcia stożka.
. Oblicz miarę kąta rozwarcia stożka.

